Chapter: Civil : Principles of Solid Mechanics : Strain and Stress
Components at an Arbitrary Orientation (Tensor Transformation)
Components at an
Arbitrary Orientation (Tensor Transformation)
In the previous sections, for
convenience, the strain and stress tensors have been developed in Cartesian, x,
y, z, coordinates drawn with the x and y
horizontal and vertical in the 'plane-of-the-paper.' We know, however, that
this orientation at a point is completely arbitrary, as is implied by indicial
notation where ij can take on values r, ?, ? or a,b,c,
or 1,2,3, or x,y,z depending on the global coordinate
system we choose. Second-order tensors (diadics) are simply a combination of
nine vector component magnitudes (3 vectors) on orthogonal planes. Thus, as we
would expect for vectors, each component transforms into a new value as the
coordinate rotates by sine and/or cosine relationships. We will derive them for
the stress tensor because most of us find it easiest to visualize forces and
use equilibrium arguments. The results are completely general, however, and
apply to any symmetric tensor. In par ticular, they apply to the strain tensor
where the normal components
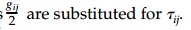
Consider a new orientation x',y',
z' which would result if the 'stress block' were
sliced out of the structural blob in a different orientation ( n correspond-ing
to x' in Figure 2.3e). In
other words the new x'
coordinate axis is rotated ?x, ?y, ?z,
as shown in Figure 2.4. Rather than use the angles directly, let their
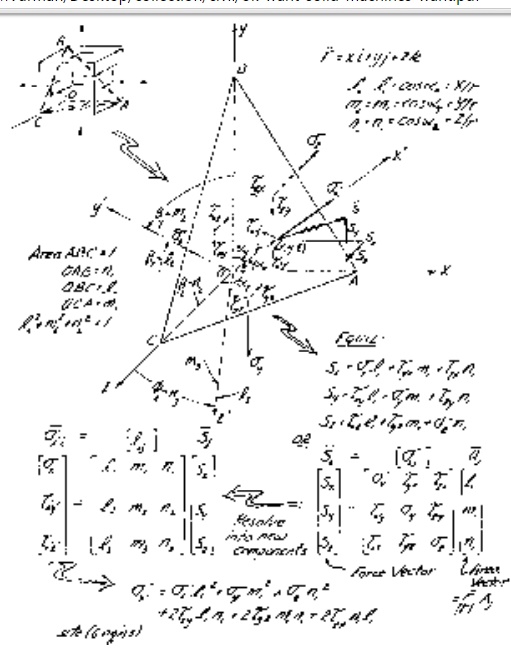
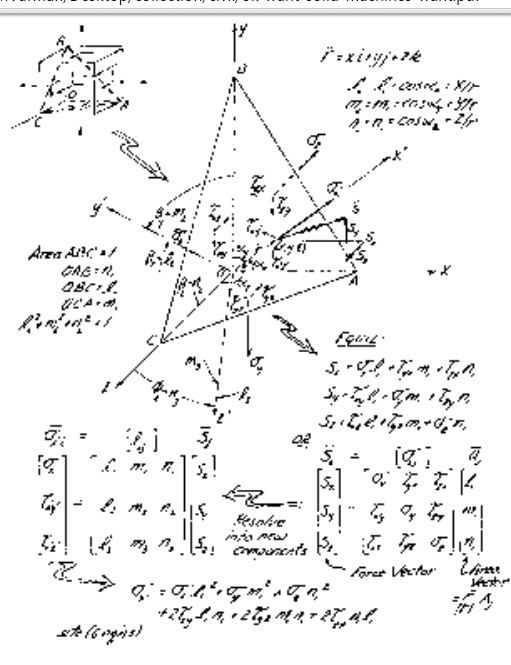
The direction cosines are not mutually
independent but can be reduced to three independent variables by six
relationships:
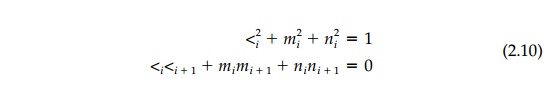
The direction cosines also represent the
areas of the faces of the tetrahe-dron. Therefore, referring to Figure 2.4, the
total force S Bar on the new exposed x' face ABC with area 1.0
can be found by equilibrium to be:
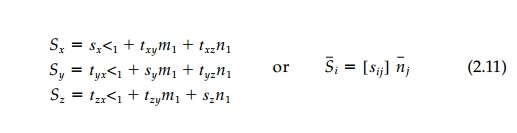
where nj has the direction cosines l1,
m1, n1 as components.
![]()
![]()
As the final step, the force S on
the x' plane can be
'dissolved' back into the new stress components ?x_,
?x_y_,
?x_z_
by again using the direction cosines:
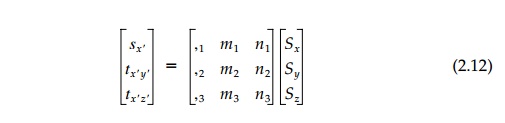
This same procedure of cutting new
tetrahedrons to expose faces with normals in the y' and z'
directions will produce the complete set of 3D
transformations in Equation (2.13) as
follows:
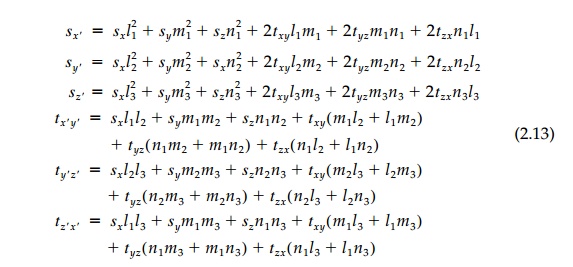
In indicial notation these
transformation equations, which provide an ana-lytic test for second-order
tensors, can be written:
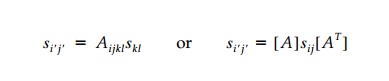
showing that it takes a
fourth-order tensor (made up of direction cosines) to transform a second-order
tensor. In practice it is more revealing and often easier to accomplish the
transformation in two stages rather than use Equa-tion (2.13) directly. First
the 'principal' state is found and the axes are then rotated, if necessary,
from there. Usually the engineer is most interested in the principal state
anyway since, in this orientation, the shear stresses are zero and normal
components take on their maximum and minimum values.
Invariants and Principal
Orientation
A vector can be plotted on paper in its
fundamental or principal form as an arrow with magnitude and direction. It can
then be decomposed into endless sets of different x', y',
z' components analytically or graphically by the
paral-lelogram law (cosines), each orthogonal set representing the same
vector. Equations (2.13) demonstrate the same essential property for tensors
(which are, after all, just a combination of vectors) but there is no neat
graphical rep-resentation in 3D, or at least it is not directly apparent. At
the same time we know that 'the point' cannot feel anything different between
one set of com-ponents or another equivalent set at some new orientation. Thus,
although a tensor can be decomposed into endless sets of different vector
components at a point, the body must actually feel the same effect regardless
of our orienta-tion when looking at it.
This fundamental description of a
tensor, not tied to any particular coordi-nate system, must involve the
'invariant' coefficients of the characteristic equation for determining the
principal values (or eigenvalues) and their directions as presented in Chapter
1 (for the general linear finite displace-ment tensor). For the stress tensor,
this characteristic Equation (1.10), is:
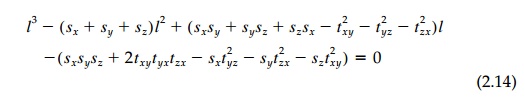
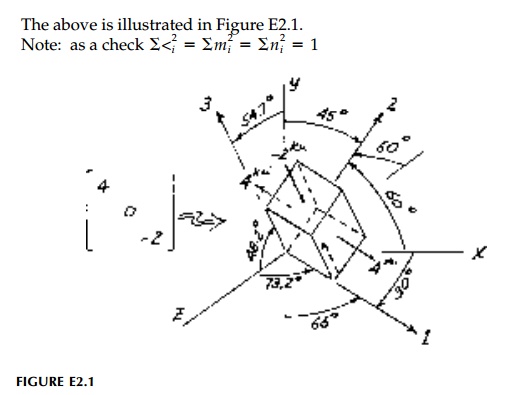
The three roots (values of ?) are the
principal stresses called ?1, ?2, ?3 and they
are real since the stress tensor (or the strain tensor) is symmetric. It is in
this principal orientation of orthogonal axes 1, 2, 3, that the tensor is
diago-nalized (no ? or ? ) and thus, in a
principal direction (say of ?1), Equation (2.11) takes the form:
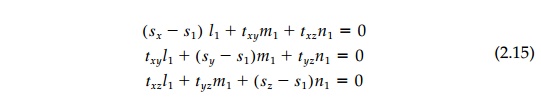
which, with the
identity l21 + n21
+
m21 = 1,
can be solved for the direction cosines (the eigenvector) giving the
orientation of the 1 or major principal axis. The same procedure is followed
with ?2 to find l2, m2, n2
and ?3 to find l3, m3, n3
giving the directions of the intermediate and minor principal stresses
respectively.
But Equation (2.14) is true for any
choice of axes and therefore the coeffi-cients must be the same in any
coordinate system. These coefficients then are the invariants:
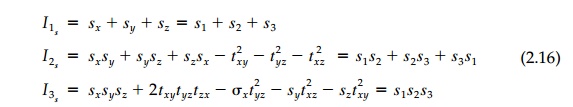
They are scalers and must be the 'fundamental
essence' of a stress tensor. The corresponding invariants of the strain tensor
can be deduced by anal-
ogy to be:
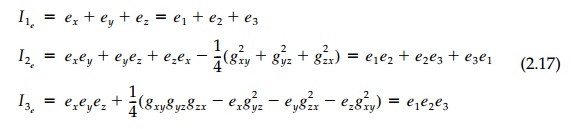
or we could write them for moment of
inertia, electromagnetic flux, or any second-order tensor.


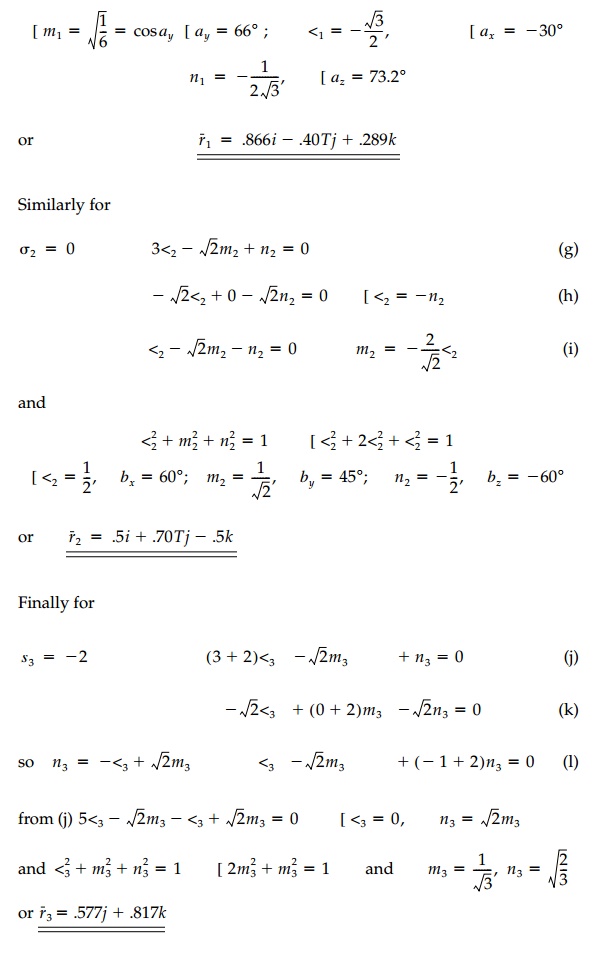
Related Topics