Equilibrium of a Differential Element

Equilibrium of a Differential Element

So far we have discussed the properties of the stress tensor and its transfor-mation with various orientations of orthogonal axes by visualizing a 'state of stress at a point' (a mathematical abstraction?). In general, in the loaded blob, stresses change over differential base lengths and to discover how they change is a primary reason that we study the mechanics of deformable solids in the first place. For design, we would like to control how stress components change along with their magnitudes, which is more difficult yet.

Consider first the free-body diagram of a differential element in rectangu-lar orthogonal coordinates x,y,z as shown in Figure 2.11. The body-force components B_x, B_y, B_z (force per unit volume) include gravity, inertial effects

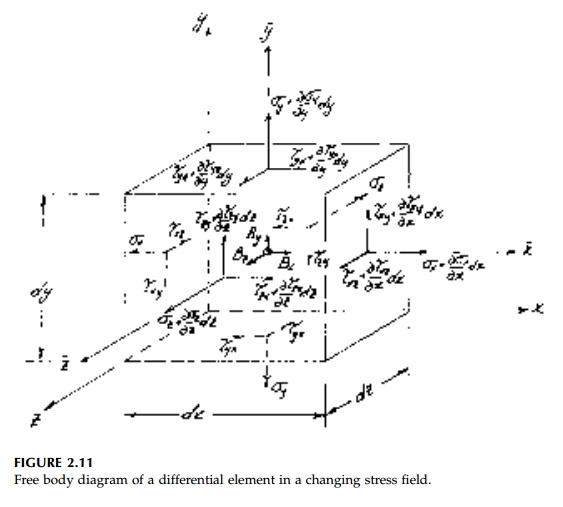
due to acceleration, magnetic fields, etc. Summing forces in the x direction:

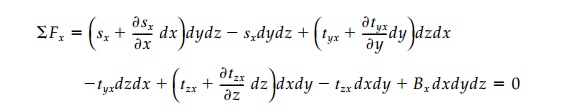
Summation of forces in the y and z directions give similar results and the three equations of equilibrium are thus:

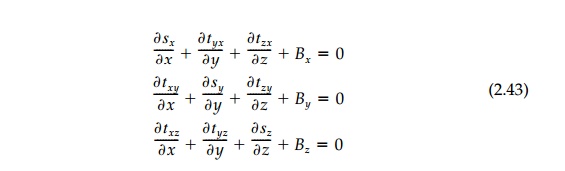
For equilibrium of the element, the sum of the moments with respect to any axis is also zero. If the centroidal axis x parallel to x is considered first:

Similar equations result from taking moments about the y and z axis. Since the terms involving differentials can be made arbitrarily small, the three moment equilibrium reduce to:

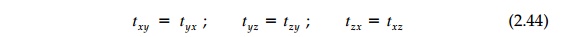
and the stress tensor is naturally symmetric* as assumed in Section 2.3.

Equations (2.43), the statement of F = ma on a differential scale, are perhaps the most important ingredients in the theory of the mechanics of deformable solids. They are field equations that apply throughout the structure, whatever its geome-try and independent of what material it is built of, the load level, or whether it is elastic, plastic, viscoelastic, or whatever. They are the starting points for all solu-tions or for design.

Unfortunately the differential equations of equilibrium are not sufficient in themselves to solve for a unique stress field for a given boundary loading. For three dimensions there are [with Equations (2.44)], three equations and six unknowns. In the plane two-dimensional case, the equilibrium equations reduce to:

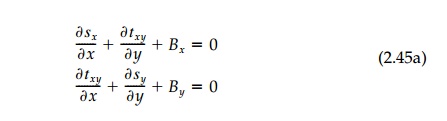
which, with two equations and three unknowns, are still insufficient. Only in the rare case of one dimension can the remaining one equation of differential equilibrium with one unknown: d?_x /dx + B_x = 0 be integrated to give a solution directly. Thus determining the stress field is inherently a statically indeterminate problem.*