Elastic Viscoelastic Analogy

Elastic-Viscoelastic Analogy

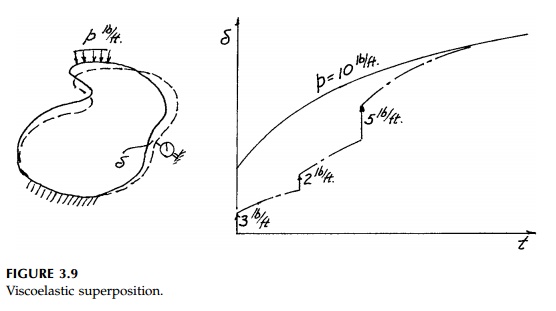
One of the most important characteristics of linear viscoelastic 'mechanical' models used to represent time-dependent material behavior is that such models obey Boltzmann's superposition principle illustrated in Figure 3.9.

The long-term creep deformation due to a loading, p, equals the sum of the deformations due to increments of p applied sequentially.

Superposition (with linearity), in turn, allows direct correspondence to elastic theory. If a solution to an elastic boundary value problem can be obtained, it can be transposed to a solution for a viscoelastic material imme-diately or by using Laplace transforms.

There are three general situations in linear elasticity:

1.The stress field is a function of only the boundary conditions, geometric shape, and loading, which are constant, i.e.,

2.  The stress field is a function of material properties (volumetric and deviatoric stiffnesses) as well, i.e.,

3.  The loads are time dependent, i.e.,

If the elastic solution is of the first type (as it is in the two-dimensional, homogeneous, isotropic situation) then there really is no problem; viscoelas-tic stresses will be the same as elastic stresses and time-dependent strains and displacements are obtained directly using G(t) and K(t) in the stress-strain relationships. In addition, Laplace transforms can sometimes be avoided in the second case for special fields, but in general it is more satisfactory to apply transform methods.* In the third situation when the loading is dynamic, Laplace transforms must be used. This may be straightforward theoretically,** but very difficult in practice since the solution in the transformed domain, where time is eliminated as a variable in both the load and the moduli, must be referred back to the real world. The inverse mapping function to do this is seldom found in standard tables, except in the simplest cases, and may be very difficult to determine from complex variables.

The main point in all this, however, is that there is a general elastic-viscoelastic analogy. Thus the simple elastic idealization is all important. When we talk about 'elastic' field theory, requirements for uniqueness and/or existence, strategy and tactics of elastic analysis, and procedures for closed-form and numerical solution for elastic problems, we are talking about far more than is implied by the word, 'elastic.' The introduction of time as a variable through linear viscos-ity (and/or loads that change with time) makes the mathematics much more involved, but the formulation directly corresponds to elasticity. Thus there is no real need to differentiate linearly viscoelastic materials from linear elastic mate-rials in a fundamental way, or consider the two separately hereafter.

Moreover, simple elastic analysis is the basic ingredient for nonlinear anal-ysis by numerical methods. Nonlinear or temperature-dependent material properties (and geometric nonlinearity due to large finite strains***) intro-duce difficulties so severe that a closed-form solution becomes intractable.

Field equations incorporating each or all of these nonlinear effects can be for-mulated, but they are so complicated that it is, today, a waste of time to even try to solve them. Instead, all types of nonlinearity can be handled satisfactorily to any degree of accuracy with a piecewise linear approximation if a powerful enough computer is available. The loads are increased incrementally and the material properties adjusted. If necessary, the geometry is revised after each step before the elastic solution is again used for the next increment.