Linear Viscous Behavior

Linear Viscous Behavior

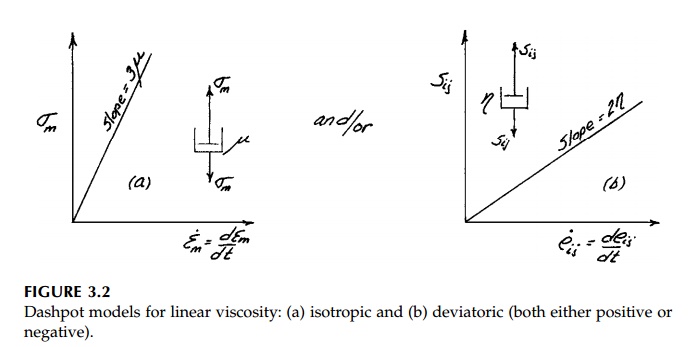
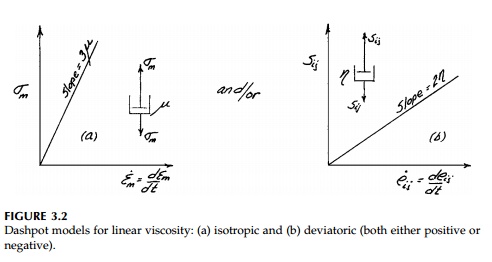
Such time-dependent stiffness (the resistance through induced stresses to the time-rate-of-change of strain) is called viscosity. If this relationship between stress and strain rate is proportional, the material exhibits Neutonion or linear viscosity. Such ideal behavior, shown in Figure 3.2, is generally observed in the laboratory to a reasonable degree at least at moderate strain rates for fluids just as linear elastic response is so common for solids at moderate strains.

The linear viscous stiffness element called a 'dashpot,' physically represents a piston in a sleeve where the surrounding viscous fluid is expelled (in com-pression) or sucked into the chamber at a rate dependent on the size of the gap between the piston and the sleeve (through which the fluid must flow). Real dashpots, often used as shock absorbers, are usually filled with oil as the work-ing fluid (silicone oil is a good choice because it is relatively inert and temper-ature insensitive) and the viscous stiffness is controlled by the size of holes drilled through the piston as well as the gap around it.

Two dashpots, one for the isotropic viscosity, , (corresponding to the elastic bulk molulus, K ) and one for the deviatoric viscosity, , (corre-sponding to the elastic shear modulus, G) are all that are necessary to rep-resent linear viscosity. By analogy:

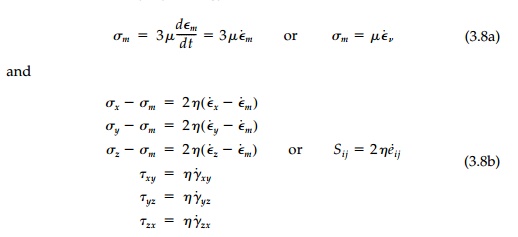
where the dot over each strain component indicates the time derivative.*

* Equation (3.8) substituted into the equilibrium equations in terms of the time derivatives of strain along with conservation of mass and energy lead to the most general equations of fluid mechanics (Navier-Stokes equations). If there is no shear stiffness ( 0), these, in turn, reduce to the Euler equations (compressible but inviscid fluids). They further reduce to poten-tial flow (or the Bernoulli equation in 1D) for incompressible, irrotational flow.

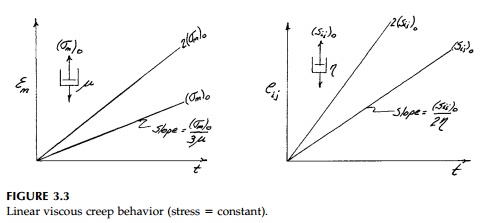
A special and very important case called creep arises if the dashpot is loaded by a constant stress( _m )_o or ( S_ij )_o. For creep the stress-strain relationship can be integrated directly and, as shown in Figure 3.3, the strain at any time is propor-tional to the stress since the strain rate is constant. Thus a highly viscous fluid can be thought of as having time-dependent 'elastic' moduli K(t) /t and G(t) /t in creep.