Elasticity and Plasticity

Elasticity and Plasticity

The fundamental assumption, which allows us to develop the relative deformation tensor E_{ij = ij} + _ij in previews pages, is that displacements (u, v, w) are small, continuous, and very smooth. Thus, over differential base lengths, deformations are linear. When this is no longer true (kinks develop in the displacement field) or is a bad approximation, we define that condi-tion as yield. If we couple this with the assumption of a linear stress-strain behavior* we have completed our development of a 'basic' or simple 'The-ory of Elasticity.' The yield condition provides the end point or boundary of the 'elasticity domain.' The 9 field equations (in 3D) relating strain and rotation to displacement and the 6 stress-strain relations can still be used in regions of the blob that have not yielded, but to describe the overall behav-ior, the 'Theory of Plasticity' must be introduced.** The 'field problem' of determining u, v, w throughout a structure after the 'loads' first cause yield becomes nonlinear and is very difficult in closed form (and thus one of the prime areas where numerical methods thrive). We will discuss post-yield behavior and derive approximate plasticity solutions (and a few exact ones) in later pages.

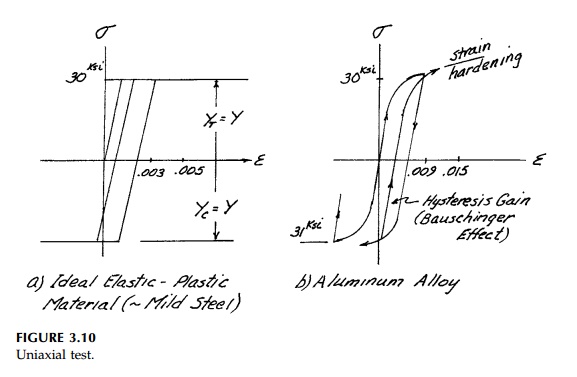
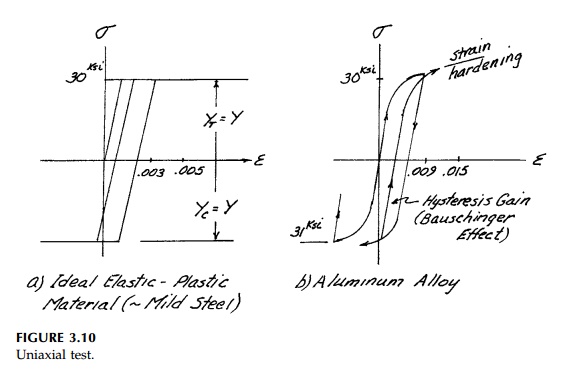
It is very important to emphasize that engineers generally do no want their structures to yield*** since once yield has occurred the structure is perma-nently deformed, residual stresses are usually introduced, and fatigue life is drastically reduced. Thus designers apply some factor of safety to the yield condition so that under 'working loads' the structure operates in the elastic range. Thus a definition of yield and its laboratory determination is as impor-tant an engineering property as E and v (or G and K) in using elastic analysis for design.