Yield of Ductile Materials

Yield of Ductile Materials

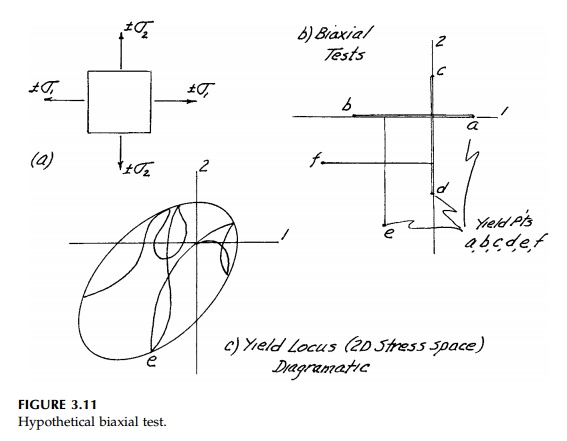
Mild steel is very nearly an ideal elastic-perfectly plastic solid for which we will use the acronym 'EPS.' A uniaxial test of an EPS would give results as shown in Figure 3.10a as compared to a less ideal material such as an aluminum alloy in Figure 3.10b. If the yield stress in tension, Y_T , is the same as compres-sion, Y_C , and there is a yield plateau, then the material is ductile and the uniaxial yield strength is characterized by a single value, Y.

Many early yield theories were based on EPS tests. These include:

a.     a. Max Stress Theory (Lame -Navier-Rankine)

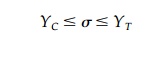
b.     b.  Max Strain Theory (St. Venant)

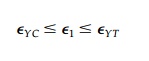
c.      c.  Max Potential Energy Theory (Beltrami)

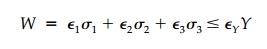
However, these ideas have been shown to be incorrect (or not general enough) since materials do not yield under isotropic compression (except perhaps at extreme values). What is actually observed in multidimensional tests is that shear causes yield.

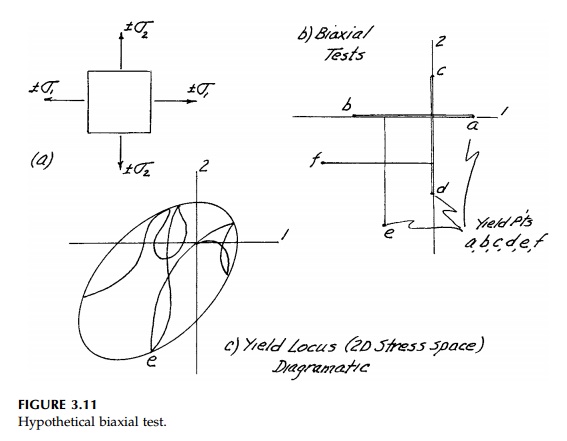
Consider first a two-dimensional, imaginary biaxial test on a solid. Simple tension and compression tests give points a and b in Figure 3.11b in the 1 direction and c and d in the 2 direction (this is not a block of EPS). However, now imagine we apply some value of ₁ < Y_T and then increase ₂. Yield might occur at point e. Doing this for various combinations of ₁ and ₂ we can develop a 'yield Locus' in 2D stress space (actually looking down the 3 axis), which separates elastic from plastic behavior for this hypothetical material. Since behavior is linear in the elastic domain, this locus will be 'independent of path' as diagrammatically indicated in Figure 3.11c.

For the general, three-dimensional situation (test), the yield locus becomes a yield surface. Since we anticipate for our ideal EPS that the isotropic pres-sure or mean stress will not affect yield, any point on this yield surface should be parallel to the line 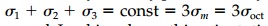 which we know is the principal-space diagonal. Looking down this orientation we would see an

octahedral plane on which a yield locus would represent only the deviatoric component or shear at yield. Thus, as shown in Figure 3.12a, the yield surface is a prism generated by sliding a yield locus in the octahedral plane along the space diagonal perpendicular to it.

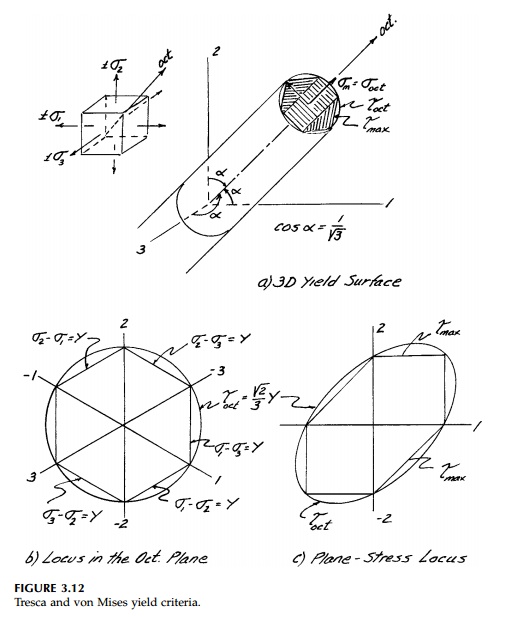
Two theories or yield conditions based on test results, which are used to describe the shape and size of this shear locus* (or cross-section of the prism) in the octahedral plane, are compared in Figure 3.12. They are:

a)     Maximum Shear Stress Theory (Tresca)

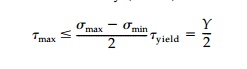
b)Octahedral Shear Stress Theory (Mises)

Essentially _oct is related to the root-mean-square of the principal stress differ-ences and _max concerns only the largest value.*

Using the uniaxial test as the 'benchmark,' the maximum difference between

the two is approximately 15% and the _max criterion as defined is always conservative. Many tests have shown that, for metals, the _oct criterion is better,

but the Tresca criterion is generally used in practice because it is conservative, easier to visualize in terms of Mohr's Circle, and usually easier to compute.