Yield(Slip) of Brittle Materials

Yield (Slip) of Brittle Materials

So far we have assumed that our material has equal yield strength in tension or compression. However, this is never quite true even for pure metals and mild steel. All materials, in fact, have a somewhat higher yield strength in compres-sion than in tension and, if this difference is pronounced, the material is brittle.** Common engineering materials of this sort are cast iron, concrete, rock, and soil, including sand, which has no tensile strength whatsoever.

The simplest conceptual model for a brittle material is to visualize that all materials have two types of shear strength:

a)  Natural or inherent strength due to primary and/or secondary bonds that glue together atoms, molecules, crystals, or particles, and

b)  Dry friction or Coulomb friction.

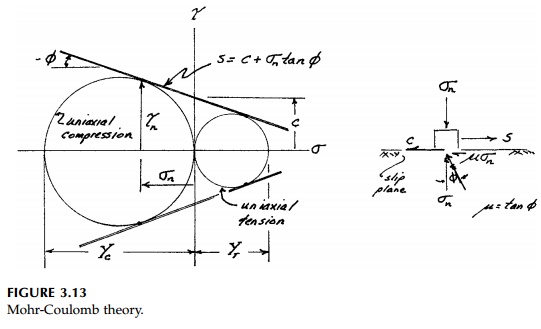
Coulomb recognized and incorporated them both in his more powerful ver-sion of the Tresca theory. Because it is best described in terms of Mohr's Circle, this elegant and unifying concept is today called the Mohr-Coulomb Theory.

The simplest version is shown in Figure 3.13. It will be discussed in much more detail later since it represents all engineering materials to a reasonable

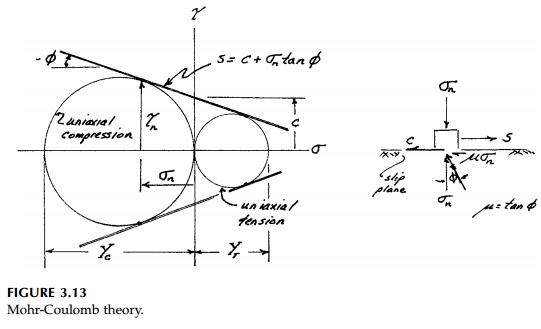
approximation. In terms of a rheological model, the simple EPS must now include the normal stress __n on the slip plane, which adds a component to the strength proportional to the coefficient of friction. Thus the Mohr-Coulomb criterion is written:

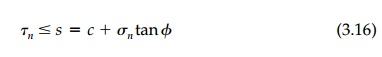
which is the envelope of the Mohr Circles for each test in stress space. The 'cohesion,' c, represents the inherent or natural shear strength which, for a ductile EPS, would be Y/2. The Mohr-Coulomb criterion is, therefore, non-linear. For easier computations it can be stated in terms of _max or _oct rather than the shear stress on the actual slip surface, _n.

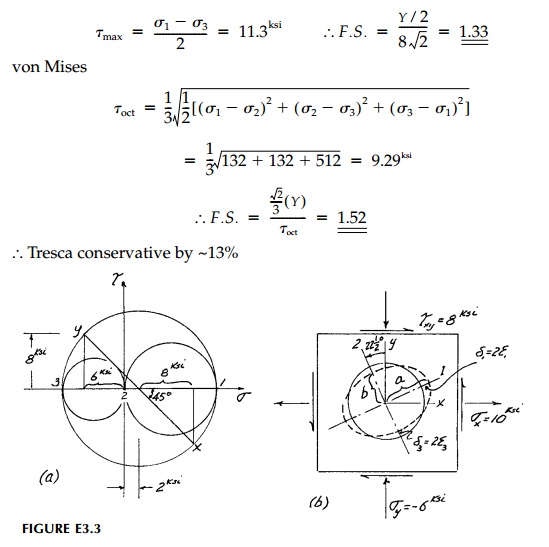
Example 3.3

A plate (plane stress) is subjected to the constant stress field: