Chapter: Civil : Principles of Solid Mechanics : Stress-Strain Relationships (Rheology)
Linear Elastic Behavior
Linear Elastic Behavior
A material specimen put
under load deforms and with sensitive instruments we can measure, at a given
time and temperature, its new shape. The first and sim-plest response
idealization is linear-elastic behavior. If, in our test, we increase the load
and the deformations increase proportionately, the material is linear. If we
unload the specimen and it returns to its original shape, it is also elastic.
Hooke was the first to do experiments of this sort and to recognize that this
fun-damental concept, now called Hooke's Law,* defining a linear
load-deformation relationship could lead to revolution in structural mechanics.
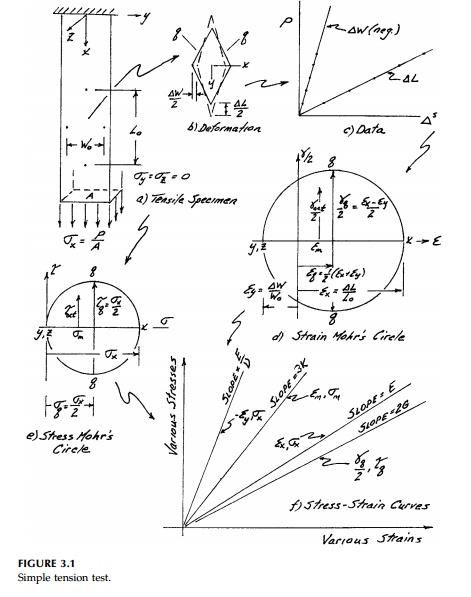
The uniaxial tension test used by Hooke has become
standard because it is so simple. If we measure and plot the deflection, ![]() ,
of bars with different lengths and cross-sectional areas under increasing load,
P, we obtain a variety of straight lines for P vs.
,
of bars with different lengths and cross-sectional areas under increasing load,
P, we obtain a variety of straight lines for P vs. ![]() .
Young* was apparently the first to divide the load by the area and the
deflection by the length to make all these lines coincide for a given material.
Although he may not have quite realized it at least originally, Young thereby
related normal stress to normal strain in the same direction by the
portionality constant, E, now named after him.** In the simple tension
test shown in Figure 3.1, the lateral con-traction
.
Young* was apparently the first to divide the load by the area and the
deflection by the length to make all these lines coincide for a given material.
Although he may not have quite realized it at least originally, Young thereby
related normal stress to normal strain in the same direction by the
portionality constant, E, now named after him.** In the simple tension
test shown in Figure 3.1, the lateral con-traction ![]() W
can be measured and is found to be proportional to the longi-tudinal elongation
W
can be measured and is found to be proportional to the longi-tudinal elongation ![]() L.
Dividing by the original base lengths, W0 and L0,
to
L.
Dividing by the original base lengths, W0 and L0,
to
'When
the Master introduced Young to his tutors, he jocularly said:
'I have brought you a pupil qualified to
read lectures to his tutors.' This, however, he did not attempt… He never
obtruded his various learning in conversation; but if appealed to on the most
difficult subject, he answered in a quick, flippant, decisive way, as if he was
speaking of the most easy; and in this mode of talking he differed from all the
clever men that I ever saw. His reply never seemed to cost him an effort, and
he did not appear to think there was any credit in being able to make it. He
did not assert any superiority, or seem to suppose that he possessed it; but
spoke as if he took it for granted that we all understood the matter as well as
he did… His language was correct, his utterance rapid, and his sentences,
though without any affectation, never left unfinished. But his words were not
those in familiar use, and the arrange-ment of his ideas seldom the same as
those he conversed with. He was, therefore, worse calculated than any man I
ever knew for the communication of knowledge… It was difficult to say how he
employed himself; he read little, and though he had access to the College and
University libraries, he was seldom seen in them. There were no books piled on
his floor, no papers scattered on his table, and his room had all the
appearance of belonging to an idle man… He seldom gave an opinion, and never
volunteered one. A philosophical fact, a difficult calculation, an ingenious
instrument, or a new invention, would engage his attention; but he never spoke
of morals, of metaphysics, or of religion.'
This quotation is taken from a biography of Young by
G. Peacock, London, 1855.
** Actually Young talked about 'weight of the
modulus,' AE, and the 'height of the modulus,' LE, which is
typical of his penchant for insight expressed with confusion (in this case
confusing the modulus, E, which relates stress to strain and the
stiffness or spring constant AE/L relating load to deformation).
This inability to express his ideas to persons of lesser intelligence
(practi-cally everyone) led to his failure as a lecturer at the Royal Institute
where, in 1801, he was appointed professor after his famous discovery of the
interference of light and prompt election as a member of the Royal Society.
Thus Young was forced to resign his professorship after two years but continued
his research on all fronts. He not only considered axial loads but suggested a
proportional relationship between shear stress and angle of twist in torsion
(the shear modu-lus), recognized the Poisson ratio effect, and noted that the
onset of yielding and permanent set was the logical limit for design. He
explained in detail the combined bending and buckling of beams and columns
solving all sorts of practical problems, but his work was unrecognized until
Lord Rayleigh reviewed it 100 years later when he gave similar lectures at the
Royal Institute. For example, Young's estimate of the molecular diameter as 2
to 10 x
10-9
inches anticipated Kelvin's similar estimate by 50 years, but it went
unnoticed.
reduce the data to normal engineering strain, the
proportionality factor, ![]() , relating them is
called Poisson's ratio.* Thus in simple tension (or com-pression):
, relating them is
called Poisson's ratio.* Thus in simple tension (or com-pression):
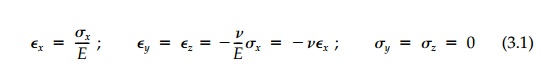
with x, y,
z principal as there are no shears. Since a uniaxial test includes both
isotropic and deviatoric components, the data, as shown in Figure 3.1, can also
be used to relate both the individual distortional components eij
to sij term by term** and the volumetric behavior, ![]() m
to
m
to ![]() m
.
m
.
Finally, effects of
temperature can be included. If the 'blob' is free to expand or contract and
the temperature change is uniform, only the volume changes and no additional
stresses result. However, if there are redundant external restraints or thermal
gradients, the stress field will also be affected. On a differential scale,
temperature changes, ![]() T,
do not directly affect the deviatoric components of stress since there is no
distortion of a differential element by
T,
do not directly affect the deviatoric components of stress since there is no
distortion of a differential element by ![]() T.
Thus the term
T.
Thus the term ![]() i
=
i
= ![]()
![]() T
can be incorporated directly in the relationship between normal strains and
stresses*** (
T
can be incorporated directly in the relationship between normal strains and
stresses*** (![]() being the coefficient
of thermal expansion).
being the coefficient
of thermal expansion).
Implicit in our discussion of a simple tension test
(Figure 3.1) is the assump-tion that the specimen represents a material that is
isotropic (the same in all directions) and also homogeneous (the same at all
points). If this were not the case, the proportionality constants would need
subscripts and as many as 36 such subscripted 'moduli' (not including ![]() )
might be necessary to define linear elastic behavior. However, for isotropic
materials, many nice Thus Young like Hooke (whom he called the 'greatest of all
philosophical mechanicers') was not appreciated by his contemporaries and while
he may have had major impact on the development of structural design and the
development of elasticity through personal interac-tion with good friends such
as John Rennie or conversations with Navier (who came to England seeking his
help more than once), there was little immediate recognition. Nor did he look
for scientific acclaim. Devoid of arrogance, even ambition, he was unable and
uninter-ested in promoting his ideas developed primarily for the
self-gratifying pleasure of satisfying his prodigious mind.
)
might be necessary to define linear elastic behavior. However, for isotropic
materials, many nice Thus Young like Hooke (whom he called the 'greatest of all
philosophical mechanicers') was not appreciated by his contemporaries and while
he may have had major impact on the development of structural design and the
development of elasticity through personal interac-tion with good friends such
as John Rennie or conversations with Navier (who came to England seeking his
help more than once), there was little immediate recognition. Nor did he look
for scientific acclaim. Devoid of arrogance, even ambition, he was unable and
uninter-ested in promoting his ideas developed primarily for the
self-gratifying pleasure of satisfying his prodigious mind.
* S. D. Poisson (1781-1840), while not a pioneer in
the formulation of the Theory of Elasticity to the extent that his
contemporaries Navier and Cauchy were, was the first to recognize the
fun-damental phenomenon of dilitational and deviatoric stress waves as well as
formulate the basic equation for plate bending. Poisson also worked on the
vibration of plates where he seems to have introduced the concept of using
trigonometric series. He takes his ratio v=- Ey
/Ex
from the tension test as 1/4 in most of this work.
**
Actually the shear modulus, G, is
usually found from a separate, purely deviatoric experi-ment such as simple
torsion or a biaxial test with equal tension and compression. Similarly a
purely isotropic test to determine the bulk modulus, K, can be run in a
triaxial cell by measuring the volume change with increasing increments of
hydrostatic stress. However, this is a very dif-ficult test in practice and
usually K is computed from E and v.
It is often easier in linear analysis to solve the
thermal stress-strain field separately and superimpose with the field due to
the applied loads.
things happen. Any state of stress or strain can be
transformed to its prin-cipal representation (without shear components).
Considering this orienta-tion, the principal directions for stress and strain
must coincide and therefore the same is true for any other orientation of
orthogonal axes. Thus we can add together three simple tension tests [Equation
(3.1)] in orthogonal directions to derive the general 3D constitutive
relationships:

where x, y,
z could just as well be r, , z or a, b, c,
or any set of orthogonal coor-dinates. Superposition used at the stress-strain
level with isotropy applies as well for the load-deformation behavior of a
homogeneous body. The inverse equa-tions for stresses in terms of strain
components, also given in Equations (3.2), are very useful for converting
experimental data and for expressing displace-ment boundary conditions in terms
of stresses.
These 'coupled,' linear-elastic constitutive
relationships between vec-tor components of the total stress and strain
tensors are often the easiest to use. Conceptually it is much better, however,
to think in terms of the separate isotropic and deviatoric components. A clue
to this insight is that the off-diagonal terms are already uncoupled in that only
one modulus, G, is involved. It is easy to show using Equation (3.2)
that the deviatoric terms, 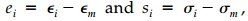 , are related in the same way and derive the relationship:
, are related in the same way and derive the relationship:

Similarly, the relationship between the scalar
isotropic components

is obtained by adding together the three normal
stress-strain relationships in terms of E and v.
Thus Equation (3.2) can be written:
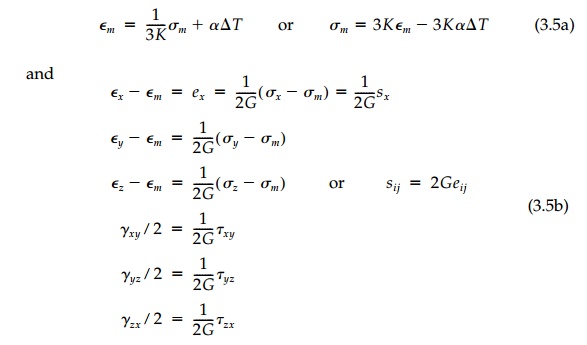
The plane-stress and
plane-strain relationships are easily extracted from Equations (3.2). Without ?T
they are
a)
For Plane Stress:
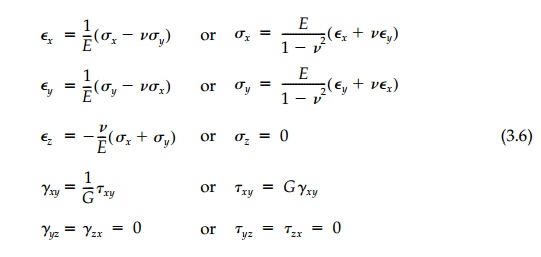
b)
and for Plane Strain:
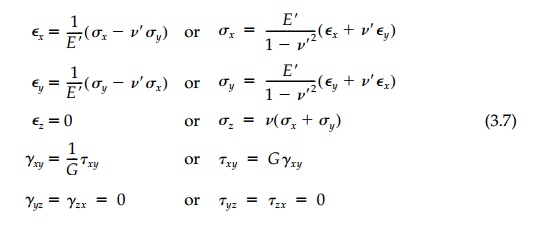
where the fictitious plane-strain moduli are defined
as:
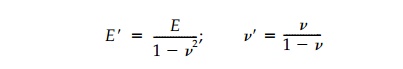
These equations show
that the in-plane equations are the same form in both cases which is, as
we will see, very significant when it comes to finding 2D fields either
analytically or experimentally. It is also interesting to note that G
and K are not affected by the assumption of plane stress or plane strain
giving the same result whether E and v
or E' and v' are substituted into
Equations (3.3) and (3.4).
It seems from Equation
(3.5) that materials respond to volumetric (hydro-static) tension or
compression quite independent of their distortional (shear-ing) behavior. As
noted previously, nature seems to favor simplicity and we should not be
surprised that isotropic and deviatoric behavior are uncou-pled. Each component
is modeled separately by a simple spring and materi-als can have totally dissimilar
isotropic and deviatoric stiffness. At one extreme is the perfectly elastic
solid where both K and G values are generally of the same order
of magnitude, and at the other extreme are liquids and gas-ses where K
can still be large under hydrostatic pressure while G is nearly zero.
For fluids, the only way significant shear stresses can develop is if
sig-nificant velocities of shear deformation are imposed.*
* And thus we come to the fundamental division of
fluid mechanics (G 0) from solid mechanics. If G 0 there is no
direct resistance to deviatoric stress (no shear stiffness) and the material
must flow until equilibrium is achieved through viscous resistance and/or
inertial forces. Although, for fluids, conservation of momentum, conservation
of mass, and some equation of state also must be consid-ered separately, the
basic field equations of equilibrium and compatibility still apply. Thus one
might think it would be economic to maintain this correspondence and learn both
subjects simultaneously. Books and courses on 'continuum mechanics' do in fact
periodically appear trying to accomplish this but they never catch on. Some
scholars after years of effort do eventually achieve this synthesis and can
visualize and enjoy roving around in the unified world of mechanics. It is
worthwhile to rec-ognize this goal and strive for it, but to present the
unified theory in all its complexity first and then work down to specific cases
later, does not seem to be a fruitful pedagogical strategy. Presenting 'the big
picture' first tends to destroy motivation and, more importantly, is not in
tune with the way the normal human mind works which, like a good computer
routine, debugs and perfects subroutines before assembling them into a general
program.
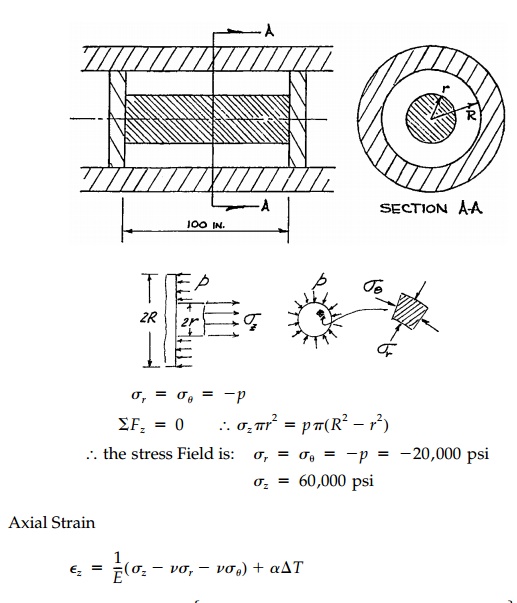
Example 3.1
An air chamber in a circular pipe is formed between
two circular plates con-nected by an aluminum rod as shown. The rigid circular
plates are assumed to fit the rigid pipe exactly so that no air can escape from
the chamber but they are free to slide along the pipe. Suppose the temperature
has been raised 150 oF and air pressure is
increased by 20,000 psi. Radius of the pipe R 20 in., radius of the rod r
10 in., initial length of the rod L 100 in., and the mate-rial
properties of the rod are 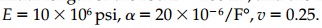 ,
v=0.25. Find the length change of the aluminum rod.
,
v=0.25. Find the length change of the aluminum rod.
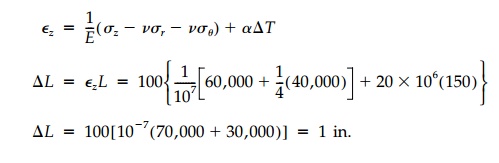
Related Topics