Methods of producing induced emf

Methods of producing induced emf

We know that the induced emf is given by the expression

Hence, the induced emf can be produced by changing

              i.          the magnetic induction (B)

            ii.            area enclosed by the coil (A) and

         iii.            the orientation of the coil (θ) with respect to the magnetic field.

1. Emf induced by changing the magnetic induction.

The magnetic induction can be changed by moving a magnet either towards or away from a coil and thus an induced emf is produced in the coil.

The magnetic induction can also be changed in one coil by changing the current in the neighbouring coil thus producing an induced emf.

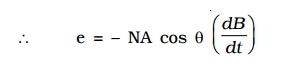
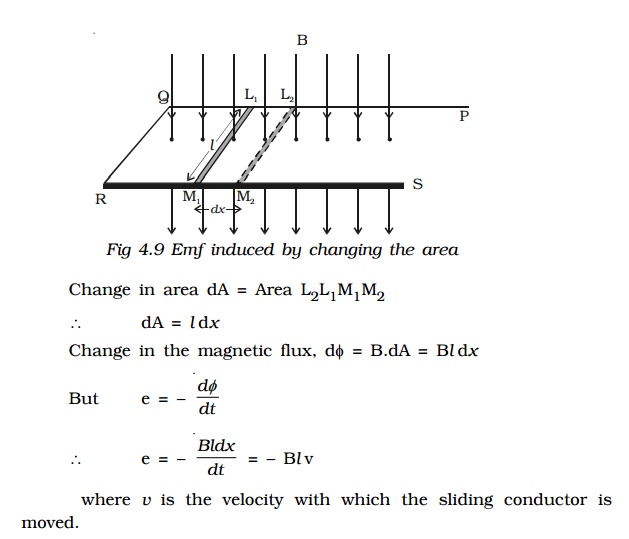
2. Emf induced by changing the area enclosed by the coil

PQRS is a conductor bent in the shape as shown in the Fig 4.9. L1M1 is a sliding conductor of length l resting on the arms PQ and RS. A uniform magnetic field ‘B’ acts perpendicular to the plane of the conductor. The closed area of the conductor is L1QRM1. When L1M1 is moved through a distance dx in time dt, the new area is L2QRM2. Due to the change in area L2L1M1M2, there is a change in the flux linked with the conductor. Therefore, an induced emf is produced.

3. Emf induced by changing the orientation of the coil

PQRS is a rectangular coil of N turns and area A placed in a uniform magnetic field B (Fig 4.10). The coil is rotated with an angular velocity ω in the clockwise direction about an axis perpendicular to the direction of the magnetic field. Suppose, initially the coil is in vertical position, so that the angle between normal to the plane of the coil and magnetic field is zero. After a time t, let θ (=ωt) be the angle through which the coil is rotated. If is the flux linked with the coil at this instant, then

 = NBA cos θ

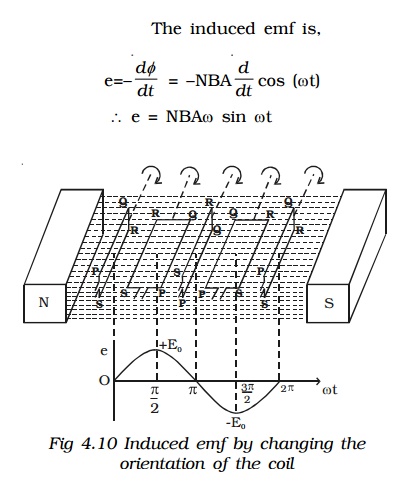
e = NBAω sin ωt     . . .(1)

The maximum value of the induced emf is, Eo = NABω

Hence, the induced emf can be represented as e = Eo sin ωt

The induced emf e varies sinusoidally with time t and the frequency being ν cycles per second (v=ω/2π)

(i) When ωt = 0, the plane of the coil is perpendicular to the field B and hence e = 0.

(ii) When ωt = π/2, the plane of the coil is parallel to B and hence e = Eo

(iii) When ωt = π, the plane of the coil is at right angle to B and hence e = 0.

(iv) When ωt = 3π/2, the plane of the coil is again parallel to B and the induced emf is e = −Eo.

(v) When ωt = 2π, the plane of the coil is again perpendicular to B and hence e = 0.

If the ends of the coil are connected to an external circuit through a resistance R, current flows through the circuit, which is also sinusoidal in nature.