Chapter: Physics : Effects of electric current : Higher Secondary(12 Std)
Ampere's Circuital Law
Ampere’s Circuital Law
Biot – Savart law expressed in an alternative way is called Ampere’s circuital law.
The magnetic induction due to an infinitely long straight current carrying conductor is
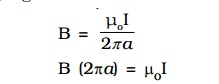
B (2πa) is the product of the magnetic field and the circumference of the circle of radius ‘a’ on which the magnetic field is constant. If L is the perimeter of the closed curve and Io is the net current enclosed by the closed curve, then the above equation may be expressed as,
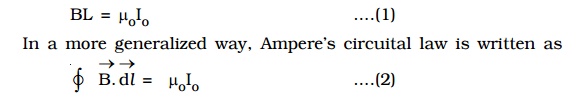
The line integral does not depend on the shape of the path or the position of the wire within the magnetic field. If the current in the wire is in the opposite direction, the integral would have the opposite sign. If the closed path does not encircle the wire (if a wire lies outside the path), the line integral of the field of that wire is zero. Although derived for the case of a number of long straight parallel conductors, the law is true for conductors and paths of any shape. Ampere’s circuital law is hence defined using equation (1) as follows :

1. Solenoid
A long closely wound helical coil is called a solenoid. Fig 3.15 shows a section of stretched out solenoid. The magnetic field due to the solenoid is vector sum of the
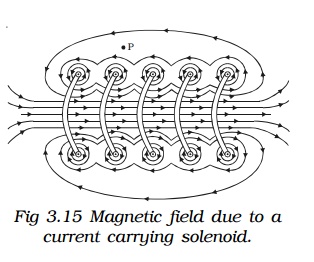
the magnetic fields due to current through individual turns of the solenoid. The magnetic fields associated with each single turn are almost concentric circles and hence tend to cancel between the turns. At the interior mid point, the field is strong and along the axis of the solenoid (i.e) the field is parallel to the axis. For a point such as P, the field due to the upper part of the solenoid turns tend to cancel the field due to the lower part of the solenoid turns, acting in opposite directions. Hence the field outside the solenoid is nearly zero. The direction of the magnetic field due to circular closed loops (solenoid) is given by right hand palm-rule.
Right hand palm rule
The coil is held in the right hand so that the fingers point in the direction of the current in the windings. The extended thumb, points in the direction of the magnetic field.

2. Magnetic induction due to a long solenoid carrying current.
Let us consider an infinitely long solenoid having n turns per unit length carrying a current of I. For such an ideal solenoid (whose length is very large compared to its radius), the magnetic field at points outside the solenoid is zero.
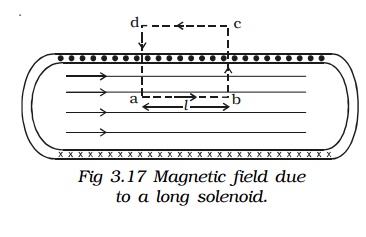
A long solenoid appears like a long cylindrical metal sheet (Fig 3.17). The upper view of dots is like a uniform current sheet coming out of the plane of the paper. The lower row of crosses is like a uniform current sheet going into the plane of the paper.
To find the magnetic induction (B) at a point inside the solenoid, let us consider a rectangular Amperean loop abcd.

Since the path of integration includes nl turns, the net current enclosed by the closed loop is

The solenoid is commonly used to obtain uniform magnetic field. By inserting a soft iron core inside the solenoid, a large magnetic field is produced
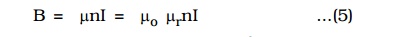
when a current carrying solenoid is freely suspended, it comes to rest like a suspended bar magnet pointing along north-south. The magnetic polarity of the current carrying solenoid is given by End rule.
End rule
When looked from one end, if the current through the solenoid is along clockwise direction Fig 3.18a, the nearer end corresponds to south pole and the other end is north pole.

When looked from one end, if the current through the solenoid is along anti-clock wise direction, the nearer end corresponds to north pole and the other end is south pole (Fig 3.18b)
Related Topics