Heating requires energy - Aquaculture Engineering

Heating requires energy

A supply of energy is needed to heat water. Energy can be transferred in three different ways: by radiation, by conduction or by convection. Electromagnetic radiation from the sun or an electric heater, for example, will be partly absorbed when it falls on a substance and become internal energy. With conduction, the energy is transferred between solids or liquids as vibrational energy of the atoms or mole-cules. Additionally, in materials with a supply of ‘free’ electrons, e.g. metals, these electrons share in any energy gain resulting from a temperature rise and their velocities increase more than those of atoms or molecules, so energy is quickly transferred to other parts. For example, when the end of an iron bar is heated, the energy will be transferred to the whole bar and after a short while it will be hot along its entire length. Convection is heat transfer result-ing from mixing of substances with different tem-peratures. Convection can be natural or forced. Natural convection occurs in water as a result of density variation caused by temperature. Water is of maximum density at 4°C. If heated water is sent in below colder water it will move upwards because it is less dense and natural convection will take place. Forced convection occurs when a medium such as water is exposed to an exterior force, for instance a pump or mixer.

The power (P) required for heating water is pro-portional to the flow and the temperature, and is given by the equation:

P = mc_p dt

where:

m =water flow (kg/s)

c_p=specific heat capacity (kJ/(kg °C))

dt= temperature increase for the water (°C).

The specific heat capacity is the amount of energy required to heat 1 kg water by 1°C: c_p= 4.18 kJ/ (kg °C) for freshwater and 4.0 kJ/(kg °C) for seawater. The temperature increase for the water is the difference between inlet and outlet temperatures.

A continuous power supply is required to heat the flowing water; the unit of power is normally the kilowatt (kW) and 1 kW = 1 kilojoule (kJ) per second. Therefore, it can be seen that power is rate of energy transfer.

Example

A freshwater flow of 10 l/min (0.17 l/s) is heated from its original temperature of 2°C to 10°C. What is the rate of energy transfer to the water, i.e. the power supplied?

P =mc_pdt

The mass of 1 l of water is 1 kg.

P =0.17 kg/s×4.18 kJ/(kg °C)×(10°C−2°C)

             = 5.7 kJ/s

= 5.7 kW

The total amount of energy that has to supplied during a given period or that has been used during a given period can be calculated from the power supplied multiplied by the time for which this power is used.

Q =Pt

where:

Q =total amount of energy (kilowatt-hour, kWh) P =power (kW)

t  = time over which heating takes place (h).

If this is compared to flowing water, the power (kW or kJ/s) corresponds to water flow rate (l/s), while the total energy consumed corresponds to the total amount of water which has flowed past a certain point during a given period of time.

It is the energy consumed (Q) that is paid for, be it electricity, oil or another energy source. Electricity is charged per kilowatt-hour, consumed and oil is sold by volume. The power (P) gives the energy rating of the heating equipment.

Example

Calculate the daily cost of heating the water in the previous example. The price of electricity is 0.1 €/kWh.

Q =Pt

              =5.7 kW × 24 h

              =136.8 kWh

Therefore the cost is

136.8 kWh × 0.1 €/kWh = 13.68 €.

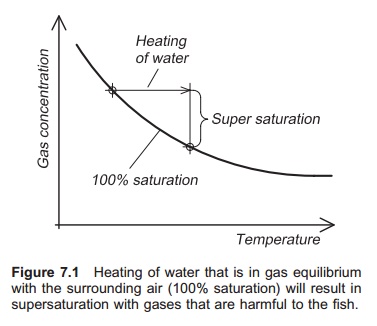
When the water is heated it must always be aerated before it is used on fish because it may become supersaturated with gas. When the water temperature increases the amount of dissolved gas is reduced. If there was equilibrium between the gases in the water and the surrounding air before the water was heated, the water will be supersatu-rated with these gases afterwards (Fig. 7.1). Nitro-gen levels will be harmful. It is very important to be aware of this, because it means that water containing fish must not be heated directly.