Composite heating systems - Aquaculture Engineering

Composite heating systems

A composite heating system is normally used to heat water for use in fish farming. The system comprises several components that all have some heating effect on the inlet water. Usually there are one or several heat exchangers in addition to either a heat pump on large farms, or a heater or an oil burner on smaller farms. The COP is calculated for the entire heating system and are usually in the range 15–25, which means that for each kW of electric energy supplied, the water is heated by 15–25 kW. Examples given below include heaters, heat pumps and heat exchangers to illustrate the profitability of using a composite heating system.

Example

Heater and heat exchanger (Fig. 7.15)

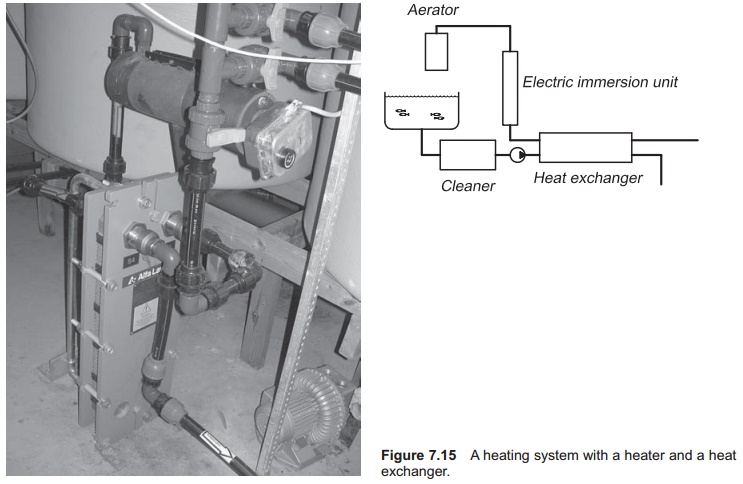
Calculate the profitability of adding a heat exchanger compared with using only an electric immersion heater in a small heating system. A water flow of 180 l/min (3 l/s) is to be heated from 4 to 8°C. The first calculation is for an electric heater alone.

Size of the heater:

P =mc_pdt

= 3 l/s × 4.18 kJ/(kg °C) × (8 − 4°C)

=50.2 kJ/s

              =50.2 kW

The daily cost of using this system with an electric-ity price of 0.1 €/kWh is:

50.2 kW × 24 h × 0.1 €/kWh = 120.5 €

Now a heat exchanger is included in the circuit to recover the energy in the outlet water; 75% recovery is quite normal. This value of course depends on the cost of the heater, heat exchanger and electricity; simu-lations should be done to find the most economical combination. If 75% of the total heat increase above 4°C is provided by the heat exchanger, 3°C of the temperature rise results from its use. This gives the following temperatures in the heat exchanger as the same amount of water flows on both sides:

Water entering heat exchanger 4°C

Water leaving heat exchanger  7°C

Water entering heater      7°C

Water leaving heater       8°C

A smaller heater is therefore needed as the water is only going to be heated from 7 to 8°C:

P =3×4.18×(8−7)= 12.5 kW

This gives the following new daily running costs:

12.5 × 24 × 0.1 = 30.0 €

As can be seen, the daily cost of heating is reduced from 120.5 to 30.0 €, a saving of 90.5 € per day, by adding a heat exchanger. This clearly illustrates the advantage of using a heat exchanger.

The necessary size of the exchanger will now be found.

Since the same amount of water is circulating on both sides of the heat exchanger, it has the following temperature programme:

Water entering heat exchanger 4°C

Water leaving heat exchanger  7°C

Water entering heater      7°C

Water leaving heater       8°C

The energy to be transferred from the warm to the cold side in the heat exchanger given by

                     = mc_pdt

              3 × 4.18 × 3

              37.6 kJ/s

For a heat exchanger the following equation applies:

P = kA LMTD

The k value for the plates in the exchanger is set to 6 kW/(m² °C) and the LMTD (temperature differ-ence that drives the heat transfer) is 1.0°C, which gives the following area:

                     = P/(k LMTD)

=37.6/(6 × 1.0)

= 6.3 m²

Assuming a plate size of width 0.4 m and height 1 m, the area is 0.4 m² (this depends on the size of plate supplied). The number of plates required = 6.3/0.4 = 15.8; this is an exchanger with 16 plates.

Example

Heater with heat exchangers in outlet water and in seawater (Fig. 7.16).

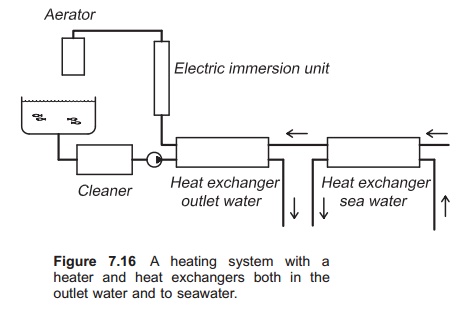
The inlet water has a temperature of 2°C and this is increased to 4°C when the water passes the seawater exchanger. The water then enters an outlet exchanger where the temperature is further increased to 9°C. The last increment up to 10°C, which is the temper-ature in the fish tank, is supplied through an electric heater. Calculate the COP of the system.

e = Q_deliverd/Q_supplied

= (t_tank−t_{raw water})/(t_tank−t_{before  heater})

= (10 − 2)/(10 − 9)

= 8

The COP is 8 for this system, so that for every kW of electric energy supplied 8 kW is supplied to the inlet water.

Example

Heat pump and heat exchanger (Fig. 7.17)

Find the profitability of installing a heat pump, com-pared with a total energy system including a heat pump and heat exchangers. A water flow of 300 l/min (50 l/s) is to be heated from 2 to 8°C. The heat pump has a COP of 5. How much electric energy must be supplied?

First, the total amount of energy that has to be trans-ferred to the water is calculated.

P =mc_pdt

= 50 l/s × 4.18 kJ/(kg °C) × (8 − 2°C)

= 1254 kJ/s

= 1254 kW

The COP is 5, meaning that the amount of energy transferred to the compressor is

1254/5 = 250.8 kW

The daily cost of using a heat pump with an elec-tricity price of 0.1 €/kWh is therefore

250.8 kW × 24 h × 0.1 €/kWh = 601.9 €

Now a heat exchanger that recovers the energy in the outlet water and transfers it to the inlet water is added to the circuit. The heat exchanger is assumed to meet 75% of the heating requirement. Of the total temperature increase of 6°C, 75% is provided by the heat exchanger, i.e. 4.5°C, which gives the following temperatures in the heat exchanger:

The new size of the heat pump can now be calculated:

P =50×4.18×(8−6.5)

= 313.5 kW

With a COP of 5, the amount of energy that must be supplied to the compressor is 313.5/5 = 62.7 kW. Therefore new daily costs are:

62.7 × 24 × 0.1 = 150.7 €

As can be seen the daily cost of heating is reduced from 601.9 € to 150.7 €, a saving of 451.2 € per day, by using a heat exchanger in addition to the heat pump. This illustrates how useful it is to utilize a heat exchanger together with a heat pump. Heat pumps are nearly always used together with one or several heat exchangers because of the large reduction in energy costs compared to the investment costs of heat exchangers.

The overall COP can now be calculated:

e = total energy transferred to thewater/electric energy supplied

= 1254 kW/62.7 kW

= 20.0

This means that of the total energy transferred to the water, only 1/20 (5%) is supplied as electric energy.