Crashing and Time-Cost Tradeoffs

Crashing and Time/Cost Tradeoffs

The previous sections discussed the duration of activities as either fixed or random numbers with known characteristics. However, activity durations can often vary depending upon the type and amount of resources that are applied. Assigning more workers to a particular activity will normally result in a shorter duration. Greater speed may result in higher costs and lower quality, however. In this section, we shall consider the impacts of time, cost and quality tradeoffs in activity durations. In this process, we shall discuss the procedure of project crashing as described below.

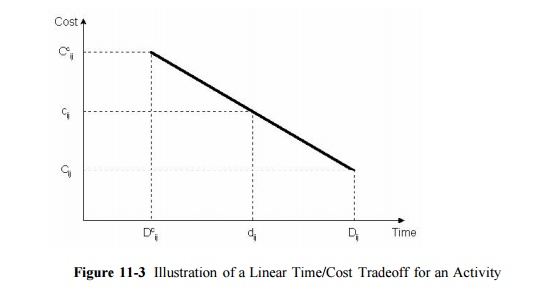
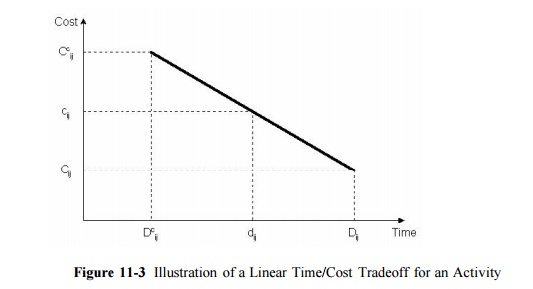
A simple representation of the possible relationship between the duration of an activity and its direct costs appears in Figure 2-3. Considering only this activity in isolation and without reference to the project completion deadline, a manager would undoubtedly choose a duration which implies minimum direct cost, represented by D_ij and C_ij in the figure. Unfortunately, if each activity was

scheduled for the duration that resulted in the minimum direct cost in this way, the time to complete the entire project might be too long and substantial penalties associated with the late project start-up might be incurred. This is a small example of sub-optimization, in which a small component of a project is optimized or improved to the detriment of the entire project performance. Avoiding this problem of sub-optimization is a fundamental concern of project managers.

At the other extreme, a manager might choose to complete the activity in the minimum possible _{time, D}c _{, but at a higher cost C}c ijij.This minimum completion time is commonly called the activity crash time. The linear relationship shown in the figure between these two points implies that any intermediate duration could also be chosen. It is possible that some intermediate point may represent the ideal or optimal trade-off between time and cost for this activity.

What is the reason for an increase in direct cost as the activity duration is reduced? A simple case arises in the use of overtime work. By scheduling weekend or evening work, the completion time for an activity as measured in calendar days will be reduced. However, premium wages must be paid for such overtime work, so the cost will increase. Also, overtime work is more prone to accidents and quality problems that must be corrected, so indirect costs may also increase. 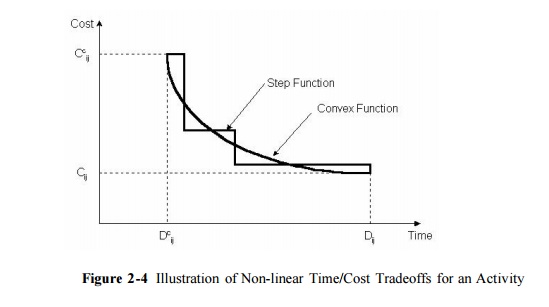More generally, we might not expect a linear relationship between duration and direct cost, but some convex function such as the nonlinear curve or the step function shown in Figure 11-4. A linear function may be a good approximation to the actual curve, however, and results in considerable analytical simplicity.

With a linear relationship between cost and duration, the critical path time/cost tradeoff problem can be defined as a linear programming optimization problem. In particular, let R_ij represent the

rate of change of cost as duration is decreased, illustrated by the absolute value of the slope of the line in Figure 11-3. Then, the direct cost of completing an activity is:

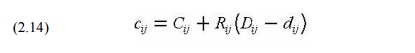
where the lower case c_ij and d_ij represent the scheduled duration and resulting cost of the activity ij. The actual duration of an activity must fall between the minimum cost time (D_ij) and the crash time (D^c_ij). Also, precedence constraints must be imposed as described earlier for each activity. Finally, the required completion time for the project or, alternatively, the costs associated with different completion times must be defined. Thus, the entire scheduling problem is to minimize total cost (equal to the sum of the c_ij values for all activities) subject to constraints arising from (1) the desired project duration, PD, (2) the minimum and maximum activity duration possibilities, and (3) constraints associated with the precedence or completion times of activities. Algebraically, this is:

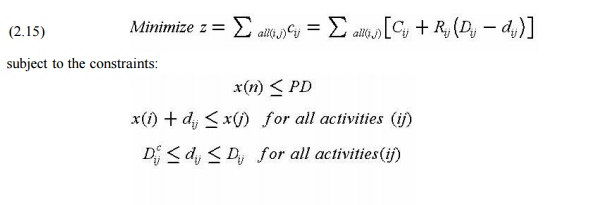
where the notation is defined above and the decision variables are the activity durations d_ij and event

times x(k). The appropriate schedules for different project durations can be found by repeatedly solving this problem for different project durations PD. The entire problem can be solved by linear programming or more efficient algorithms which take advantage of the special network form of the problem constraints.

One solution to the time-cost tradeoff problem is of particular interest and deserves mention here. The minimum time to complete a project is called the project-crash time. This minimum completion time can be found by applying critical path scheduling with all activity durations set to

their minimum values (D^c_ij). This minimum completion  time for the project can then be used in

the time-cost scheduling problem described above to determine the minimum project-crash cost. Note that the project crash cost is not found by setting each activity to its crash duration and summing up the resulting costs; this solution is called the all-crash cost. Since there are some activities not on the critical path that can be assigned longer duration without delaying the project, it is advantageous to change the all-crash schedule and thereby reduce costs.

Heuristic approaches are also possible to the time/cost tradeoff problem. In particular, a simple approach is to first apply critical path scheduling with all activity durations assumed to be at minimum cost (D_ij). Next, the planner can examine activities on the critical

path and reduce the scheduled duration of activities which have the lowest resulting increase in costs. In essence, the planner develops a list of activities on the critical path ranked in accordance with the unit change in cost for a reduction in the activity duration. The heuristic solution proceeds by shortening activities in the order of their lowest impact on costs. As the duration of activities on the shortest path are shortened, the project duration is also reduced. Eventually, another path becomes critical, and a new list of activities on the critical path must be prepared. By manual or automatic adjustments of this kind, good but not necessarily optimal schedules

can be identified. Optimal or best schedules can only be assured by examining changes in combinations of activities as well as changes to single activities. However, by alternating between adjustments in particular activity durations (and their costs) and a

critical path scheduling procedure, a planner can fairly rapidly devise a shorter schedule to meet a particular project deadline or, in the worst case, find that the deadline is impossible of accomplishment.

This type of heuristic approach to time-cost tradeoffs is essential when the time-cost tradeoffs for each activity are not known in advance or in the case of resource constraints on the project. In these cases, heuristic explorations may be useful to determine if greater effort should be spent on estimating time-cost tradeoffs or if additional resources should be retained for the project. In many cases, the basic time/cost tradeoff might not be a smooth curve as shown in Figure 11-4, but only a series of particular resource and schedule combinations which produce particular durations. For example, a planner might have the option of assigning either one or two crews to a particular activity; in this case, there are only two possible durations of interest.

Example 2-4: Time/Cost Trade-offs

The construction of a permanent transit way on an expressway median illustrates the possibilities for time/cost trade-offs in construction work. One section of 10 miles of transit way was built in 1985 and 1986 to replace an existing contra- flow lane system (in which one lane in the expressway was reversed each day to provide additional capacity in the peak flow direction). Three engineers' estimates for work time were prepared:

z 975 calendar day, based on 750 working days at 5 days/week and 8 hours/day of work plus 30 days for bad weather, weekends and holidays.

z 702 calendar days, based on 540 working days at 6 days/week and 10 hours/day of work. z 360 calendar days, based on 7 days/week and 24 hours/day of work.

The savings from early completion due to operating savings in the contra-flow lane and contract administration costs were estimated to be $5,000 per day.

In accepting bids for this construction work, the owner required both a dollar amount and a completion date. The bidder's completion date was required to fall between 360 and 540 days. In evaluating contract bids, a $5,000 credit was allowed for each day less than 540 days that a bidder specified for completion. In the end, the successful bidder completed the project in 270 days, receiving a bonus of 5,000*(540-270) = $450,000 in the $8,200,000 contract. However, the contractor experienced fifteen to thirty percent higher costs to maintain the continuous work schedule.