Calculations for Critical Path Scheduling

Calculations for Critical Path Scheduling

With the background provided by the previous sections, we can formulate the critical path scheduling mathematically. We shall present an algorithm or set of instructions for critical path scheduling assuming an activity-on-branch project network. We also assume that all precedence are of a finish-to-start nature, so that a succeeding activity cannot start until the completion of a preceding activity. In a later section, we present a comparable algorithm for activity-on-node representations with multiple precedence types.

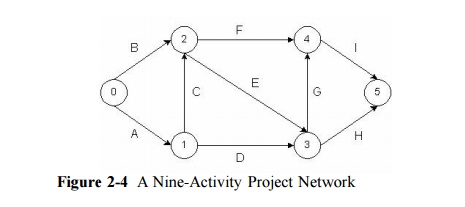
Suppose that our project network has n+1 nodes, the initial event being 0 and the last event being n. Let the time at which node events occur be x₁, x₂,...., x_n, respectively. The start of the project

at x₀ will be defined as time 0. Nodal event times must be consistent with activity durations, so that

an activity's successor node event time must be larger than an activity's predecessor node event time plus its duration. For an activity defined as starting from event i and ending at event j, this relationship can be expressed as the inequality constraint, x_j x_i + D_ij where D_ij is the duration of activity (i,j). This

same expression can be written for every activity and must hold true in any feasible schedule. Mathematically, then, the critical path scheduling problem is to minimize the time of project

completion (x_n) subject to the constraints that each node completion event cannot occur until each of the predecessor activities have been completed:

Minimize 

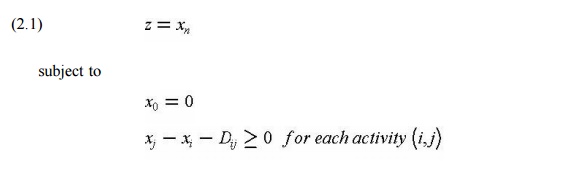
Rather than solving the critical path scheduling problem with a linear programming algorithm (such as the Simplex method), more efficient techniques are available that take advantage of the network structure of the problem. These solution methods are very efficient with respect to the required computations, so that very large networks can be treated even with personal computers. These methods also give some very useful information about possible activity schedules. The programs can compute the earliest and latest possible starting times for each activity which are consistent with completing the project in the shortest possible time. This calculation is of particular interest for activities which are not on the critical path (or paths), since these activities might be slightly delayed or re-scheduled over time as a manager desires without delaying the entire project.

An efficient solution process for critical path scheduling based upon node labeling is shown in Table 2-1. Three algorithms appear in the table. The event numbering algorithm numbers the nodes (or events) of the project such that the beginning event has a lower number than the ending event for each activity. Technically, this algorithm accomplishes a "topological sort" of the activities. The project start node is given number 0. As long as the project activities fulfill the conditions for an activity-on-branch network, this type of numbering system is always possible. Some software packages for critical path scheduling do not have this numbering algorithm programmed, so that the construction project planners must insure that appropriate numbering is done.

The earliest event time algorithm computes the earliest possible time, E(i), at which each event, i, in the network can occur. Earliest event times are computed as the maximum of the earliest start times plus activity durations for each of the activities immediately preceding an event. The earliest start time for each activity (i,j) is equal to the earliest possible time for the preceding event E(i):

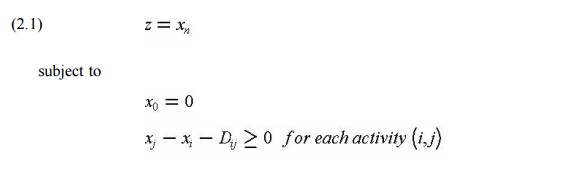
Activities are identified in this algorithm by the predecessor node (or event) i and the successor node j. The algorithm simply requires that each event in the network should be examined in turn beginning with the project start (node 0).

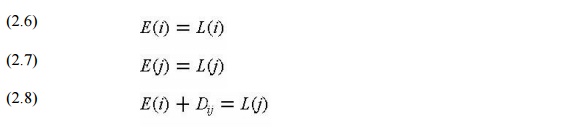
The latest event time algorithm computes the latest possible time, L(j), at which each event j in the network can occur, given the desired completion time of the project, L(n) for the last event n. Usually, the desired completion time will be equal to the earliest possible completion time, so that E(n) = L(n) for the final node n. The procedure for finding the latest event time is analogous to that for the earliest event time except that the procedure begins with the final event and works backwards through the project activities. Thus, the earliest event time algorithm is often called a forward pass through the network, whereas the latest event time algorithm is the the backward pass through the network. The latest finish time consistent with completion of the project in the desired time frame of L(n) for each activity (i,j) is equal to the latest possible time L(j) for the succeeding event:

 The earliest start and latest finish times for each event are useful pieces of information in developing a project schedule. Events which have equal earliest and latest times, E(i) = L(i), lie on the critical path or paths. An activity (i,j) is a critical activity if it satisfies all of the following conditions:

Hence, activities between critical events are also on a critical path as long as the activity's earliest start time equals its latest start time, ES(i,j) = LS(i,j). To avoid delaying the project, all the activities on a critical path should begin as soon as possible, so each critical activity (i,j) must be scheduled to begin at the earliest possible start time, E(i).

Example 2 -2: Critical path scheduling calculations

Consider the network shown in Figure 2-4 in which the project start is given number 0. Then, the only event that has each predecessor numbered is the successor to activity A, so it receives number 1. After this, the only event that has each predecessor numbered is the successor to the two activities B and C, so it receives number 2. The other event numbers resulting from the algorithm are also shown in the figure. For this simple project network, each stage in the numbering process found only one possible event to number at any time.

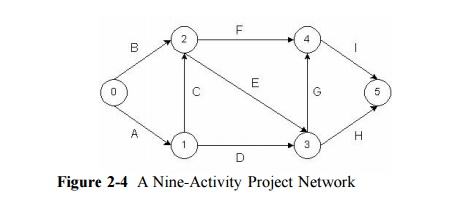
With more than one feasible event to number, the choice of which to number next is arbitrary. For example, if activity C did not exist in the project for Figure 10-4, the successor event for activity A or for activity B could have been numbered 1.

Once the node numbers are established, a good aid for manual scheduling is to draw a small rectangle near each node with two possible entries. The left hand side would contain the earliest time the event could occur, whereas the right hand side would contain the latest time the event could occur without delaying the entire project.