Activity Float and Schedules

Civil - Construction Planning And Scheduling:

Activity Float and Schedules

A number of different activity schedules can be developed from the critical path scheduling procedure described in the previous section. An earliest time schedule would be developed by starting each activity as soon as possible, at ES(i,j). Similarly, a latest time schedule would delay the start of each activity as long as possible but still finish the project in the minimum possible time. This late schedule can be developed by setting each activity's start time to LS(i,j).

Activities that have different early and late start times (i.e., ES(i,j) < LS(i,j)) can be scheduled to start anytime between ES(i,j) and LS(i,j) as shown in Figure 10-6. The concept of float is to use part or all of this allowable range to schedule an activity without delaying the completion of the project. An activity that has the earliest time for its predecessor and successor nodes differing by more than its duration possesses a window in which it can be scheduled. That is, if E(i) + D_ij < L(j),

then some float is available in which to schedule this activity.

Float is a very valuable concept since it represents the scheduling flexibility or "maneuvering room" available to complete particular tasks. Activities on the critical path do not provide any flexibility for scheduling nor leeway in case of problems. For activities with some float, the actual starting time might be chosen to balance work loads over time, to correspond with material deliveries, or to improve the project's cash flow.

Of course, if one activity is allowed to float or change in the schedule, then the amount of float available for other activities may decrease. Three separate categories of float are defined in critical path scheduling:

1.     Free float is the amount of delay which can be assigned to any one activity without delaying subsequent activities. The free float, FF(i,j), associated with activity (i,j) is:

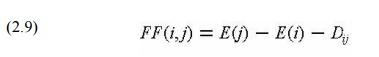
2.     2. Independent float is the amount of delay which can be assigned to any one activity without delaying subsequent activities or restricting the scheduling of preceding activities. Independent float, IF(i,j), for activity (i,j) is calculated as: (2.10)

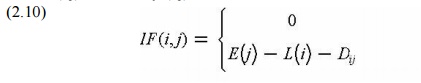
3.     3. Total float is the maximum amount of delay which can be assigned to any activity without delaying the entire project. The total float, TF (i,j), for any activity (i,j) is calculated as: (2.11)

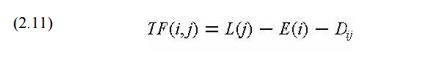
Each of these "floats" indicates an amount of flexibility associated with an activity. In all cases, total float equals or exceeds free float, while independent float is always less than or equal to free float. Also, any activity on a critical path has all three values of float equal to zero. The converse of this statement is also true, so any activity which has zero total float can be recognized as being on a critical path.

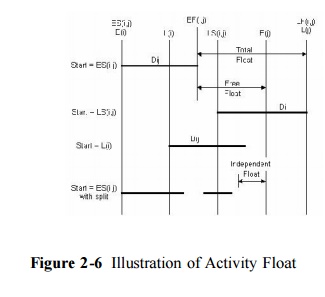
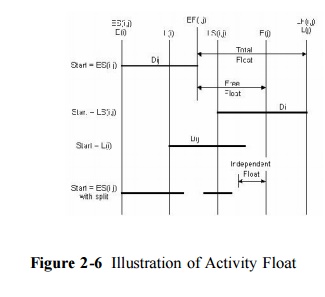
The various categories of activity float are illustrated in Figure 2-6 in which the activity is represented by a bar which can move back and forth in time depending upon its scheduling start. Three possible scheduled starts are shown, corresponding to the cases of starting each activity at the earliest event time, E(i), the latest activity start time LS(i,j), and at the latest event time L(i). The three categories of float can be found directly from this figure. Finally, a fourth bar is included in the figure to illustrate the possibility that an activity might start, be temporarily halted, and then re-start. In this case, the temporary halt was sufficiently short that it was less than the independent float time and thus would not interfere with other activities. Whether or not such work splitting is possible or economical depends upon the nature of the activity.

As shown in Table 2-3, activity D(1,3) has free and independent floats of 10 for the project shown in Figure 2-4. Thus, the start of this activity could be scheduled anytime between time 4 and 14 after the project began without interfering with the schedule of other activities or with the earliest completion time of the project. As the total float of 11 units indicates, the start of activity D could also be delayed until time 15, but this would require that the schedule of other activities be restricted. For example, starting activity D at time 15 would require that activity G would begin as soon as activity D was completed. However, if this schedule was maintained, the overall completion date of the project would not be changed.

Example 2-3: Critical path for a fabrication project

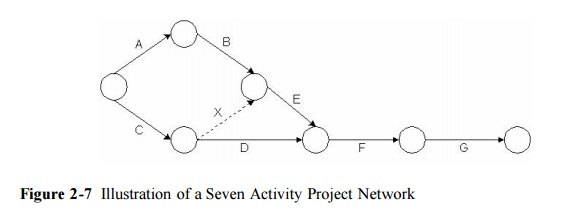
As another example of critical path scheduling, consider the seven activities associated with the fabrication of a steel component shown in Table 2-4. Figure 2-7 shows the network diagram associated with these seven activities. Note that an additional dummy activity X has been added to insure that the correct precedence relationships are maintained for activity E. A simple rule to observe is that if an activity has more than one immediate predecessor and another activity has at least one but not all of these predecessor activity as a predecessor, a dummy activity will be required to maintain precedence relationships. Thus, in the figure, activity E has activities B and C as predecessors, while activity D has only activity C as a predecessor. Hence, a dummy activity is required. Node numbers have also been added to this figure using the procedure outlined in Table 2-1. Note that the node numbers on nodes 1 and 2 could have been exchanged in this numbering process since after numbering node 0, either node 1 or node 2 could be numbered next.