Classical Conditioning: Role of Surprise

THE ROLE OF SURPRISE

In the experiments we’ve been describing, animals seem keenly sensitive to comparisonsamong probabilities. Will a dog learn to salivate in response to a beeper if the sound is fol-lowed by food only 30% of the time? The answer is yes, if food arrives less than 30% of the time when no beeper is sounded. Will a mouse shiver in response to a tone that, in the past, has been followed only half the time by a blast of cold air? Again, the answer is yes—provided that cold blasts arrive less than half the time without the warning tone.

This sensitivity to probabilities is, in fact, a widespread feature of classical condi-tioning and can be observed in creatures as diverse as humans and rabbits, pigeons and rats. In all cases, conditioning depends on whether the probability of the US after the CS is different from the probability of the US without the CS. But how is this possible? The dog and the mouse are obviously not standing by with calculators, computing these probabilities. For that matter, when we study classical conditioning in humans, our par-ticipants don’t appear to be tallying up the various types of trials and computing the rel-evant ratios. How, then, are the test subjects influenced by these probabilities?

One proposal starts with the idea that—for any organism, human or otherwise— associations can provide a basis for expectations, and learning can then take the form of an adjustment in expectations whenever a surprise occurs. To see how this plays out, imagine an animal in a learning experiment. At the very start, there’s no association between (say) the sound of the metronome and the delivery of food, and so the animal has no expecta-tion that this CS will be followed by this US. When the food does arrive, therefore, it’s a surprise; and this causes the animal to adjust its expectations. Specifically, the surprise leads the animal to a tentative expectation that, in the future, other metronome sounds might also be followed by food. This expectation will be weak at first, and so the next time this CS is followed by the US, the animal will still be a little bit surprised. This will cause another adjustment in the animal’s expectation—and so an increase in the strength of association between CS and US.

This process will then be repeated over and over as the learning experiment contin-ues. In each trial, the CS is presented; and this will trigger certain expectations in the ani-mal for what’s going to happen next. If these expectations are correct, then the arrival (or nonarrival) of the US will be no surprise, and so there’s no reason to adjust the expecta-tions (Figure 7.13). But if the expectations are wrong, then some adjustment is called for. If no US is expected but one arrives anyhow, this surprise will lead to a strengthening of the CS-US association and thus a stronger expectation the next time around. Conversely, if the US is expected but does not arrive, then the CS-US association will be weakened and so there will be a weaker expectation on the next trial.

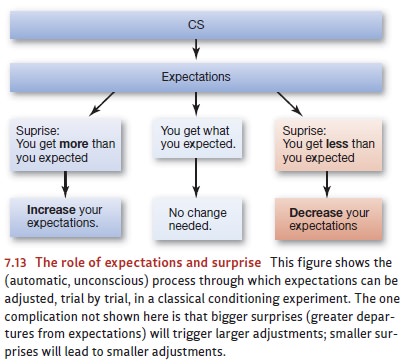
If things continue in this way, trial after trial, the expectations will be adjusted each time they’re out of step with actual events and left alone when they’re correct. Put differently, the expectations will be tuned and retuned until they’re quite accurate—fully in line with the circum-stances. Thus, if the animal is in a situation in which a CS is followed by the US 90% of the time, the animal will end up with strong expectations for what’s going to happen next, whenever it experiences the CS. If the animal is in an environment in which a CS is followed by the US only 80% of the time, or 60%, the animal’s expectations will be accordingly weaker.

Notice, then, that we can predict the animal’s behavior—in particular, whether the animal will learn or not—by keeping track of the various probabilities in the animal’s situation. But the animal has no direct knowledge about these probabilities. Instead, the animal has a set of expectations, based on its experience. The key, though, is that these expectations have been shaped, trial by trial, by an adjustment process that brings the expectations into line with reality, as shown in Figure 7.13. This is the mechanism through which the animal’s behavior ends up fully in accord with the probabilities in its environment (Kamin, 1968; Rescorla & Wagner, 1972; but see R. Miller, Barnet, & Grahame, 1995; Pearce & Bouton, 2001).

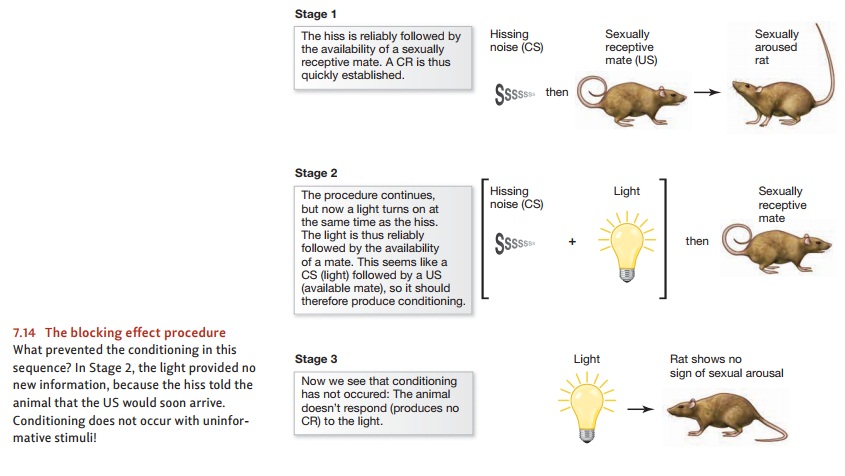
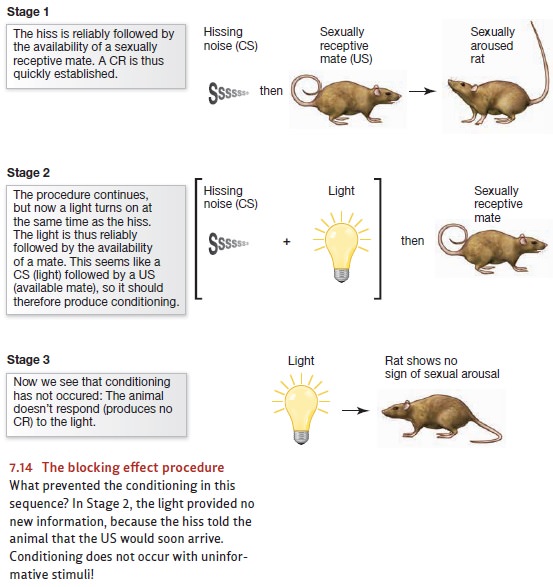
Is this proposal correct? Is this how classical conditioning proceeds, with a trial-by-trial calibration of expectations? One way to find out is to scrutinize the role of surprise, which—in the account just sketched—plays a crucial role in learning. And in fact the importance of surprise is easily demonstrated. In studies of the blocking effect, animals are exposed to a three-part procedure (Figure 7.14). In stage 1, the animals—rats, for example— hear a hissing noise that’s followed by a US (let’s say, the sight of a sexually receptive mate). As one might expect, this noise becomes a CS for sexual arousal. In stage 2, the hissing sound is still followed by this same US; but now the hissing sound is reliably accompanied by another stimulus—a bright light. The sequence in this stage, therefore, is the “package” of hiss plus light, followed by the sight of the potential mate. Then, in stage 3, it’s time for the crucial test: Now we present the light by itself and observe the rat’s response.

In stage 2 of this procedure, the light was reliably followed by the US, and we might expect this to produce learning—so that the light will now trigger the CR. But that’s not what happens. Instead, the rat doesn’t respond to the light at all. This is because in stage 2 the light provided only redundant information. The rat already knew from the hissing noise that the US was about to be presented, and so it wasn’t at all surprised when the US did arrive. As a result, the rat learned nothing about the light—clear confirmation of the proposal that learning does in fact depend on surprise and, more broadly, on the information value of the stimuli.

The blocking effect can easily be demonstrated in experiments with humans (Beckers, Miller, De Houwer, & Urushihara, 2006; Kruschke & Blair, 2000), and analogous phe-nomena can be documented outside of the laboratory. In the United States, for example, temperatures are routinely reported in degrees Fahrenheit—unlike the rest of the world, which uses the metric centigrade scale. For some years, weather forecasters tried to teach Americans the alternative scale by routinely describing the temperature with both scales: “The high tomorrow will be 75 degrees, or 24 centigrade.” “Watch out—it’s going to be cold tonight—in the teens, or –10 degrees centigrade.” This effort failed—and Americans learned nothing about the metric scale. Why? Because the centigrade number was redundant with the Fahrenheit temperature, and so the centigrade number provided no information, no surprise. As a result, Americans ignored the number—just as a rat in the laboratory ignores the redundant (and therefore uninformative) light.