Cardiac Electrophysiology: Transmembrane Potential

CARDIAC ELECTROPHYSIOLOGY

Transmembrane Potential

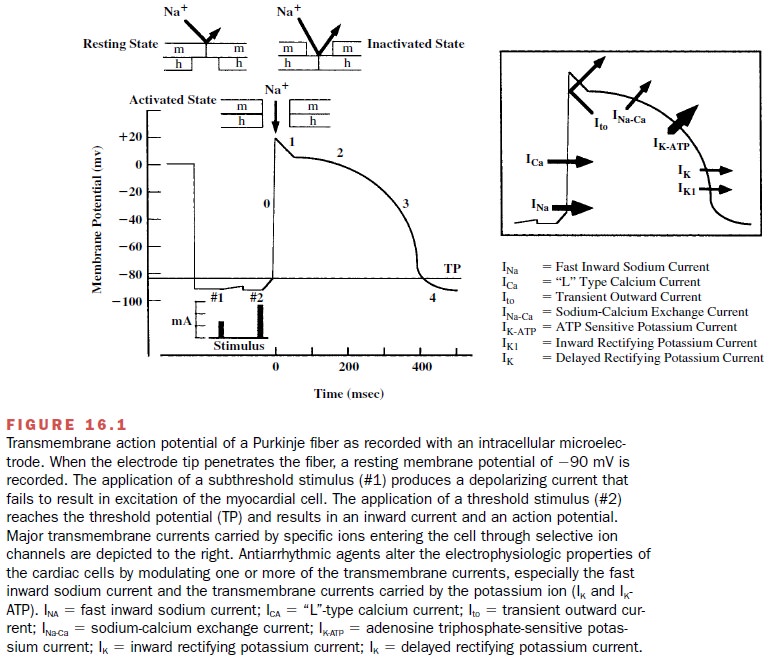
Figure 16.1 shows the phases of the cardiac action po-tential recorded with an intracellular microelectrode. The characteristic action potential is the result of acti-vation and inactivation of multiple ion channels, which allows the flow of charged ions across the sarcolemmal membrane. The ion channels are transmembrane pro-teins possessing two important features: an ion selective pore that allows the passage of a specific cation or an-ion and regulatory components that respond to chemi-cal stimulation or changes in the transmembrane poten-tial by opening or closing. The ions flow through open channels according to the electrochemical driving forces at any given moment.

Like all other electrically active cells, the interior of the cardiac muscle cell is electrically negative with re-spect to the surrounding medium. This difference be-tween the exterior and interior of a myocardial cell re-sults from the action of several energy-requiring pumps, such as the NA⁺ –K⁺ –ATPase, which pumps NA⁺ out of and K⁺ into the cell in a ratio of 3Na to 2K⁺ , and the presence of large negatively charged intracellular pro-teins that do not diffuse freely across the sarcolemmal membrane. The normal resting [K⁺ ]_i is 140 mM, whereas the extracellular K⁺ concentration, [K⁺ ]₀, is 4 mM. The resting myocardial cell tends to be highly permeable to K⁺ and less so to NA⁺ and Ca⁺⁺ ; therefore, a net diffusion of K⁺ flows out of the cell, leaving behind negatively charged proteins. As a result, the interior of t he cell becomes electronegative, and two opposing forces are established: a chemical force due to a con-centration gradient and a counteracting electrostatic force established by the negatively charged ions within the cell.

At equilibrium, the chemical and electrostatic forces are equal, and there is no net flow of ions across the sarcolemmal membrane. The membrane potential at which this occurs may be calculated using the Nernst equation:

E_x = - 61 log([x]_i/[x]_o)

In this equation, x is the ion in question, [x]_i is the concentration inside the cell, and [x]_o is the concentra-tion outside the cell. For potassium, using a [K]_i of 140 mM and a [K]_o of 4 mM, the E_K is equal to –94 mV, which is almost identical to the normal resting mem-brane potential of -90 mV. The contribution of other ionic species to the resting membrane potential is smaller because of the low transmembrane permeabil-ity at hyperpolarized resting membrane potentials.

An examination of the relationship of [K ]_o] and [K ]_i] in the Nernst equation shows that an increase in the [K ]_o will result in a decrease in the membrane rest-ing potential (less negative). Changes in the extracellu-lar concentration of another ion (NA⁺ , Ca⁺⁺ , Mg , Cl^{- )} may also modify the resting potential.

To produce membrane depolarization, a current stimulus of sufficient intensity to exceed the outward K⁺ current must be applied to the cell. If the depolariz-ing stimulus raises the membrane potential above a threshold value, sodium channels within the sarcolem-mal membrane change their conformation and open their ion-selective pore, allowing NA⁺ to enter the cell driven by the electrochemical gradient. The open sodium channels raise the membrane potential toward the equilibrium potential of sodium ( 65 mV) and set into motion the intricate and precisely coordinated se-ries of ion channel openings and closings leading to the characteristic action potential.

The action potential has been divided into five phases, rapid depolarization (phase 0), early repolariza-tion (phase 1), plateau (phase 2), rapid repolarization (phase 3) and finally the resting phase in myocytes or slow diastolic depolarization (phase 4). The last is a property in cells with the potential for automaticity (de-fined later). A brief outline of each of these phases in the normal myocyte is given next.