Aggregate Analysis

AGGREGATE ANALYSIS:

·        In fact, a sequence of n operations on an initially empty stack cost at most O(n).

·        Each object can be POP only once (including in MULTIPOP) for each time it is PUSHed. #POPs is at most #PUSHs, which is at most n.

·        Thus the average cost of an operation is O(n)/n = O(1).

·        Amortized cost in aggregate analysis is defined to be average cost.

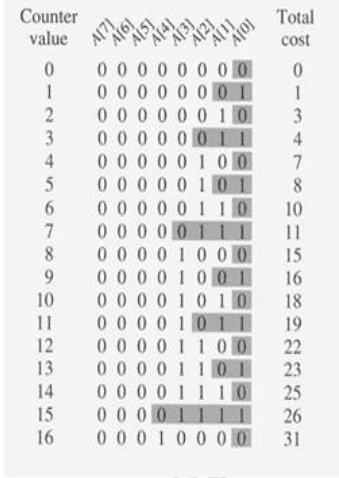
Example: Increasing a binary counter

Binary counter of length k, A[0..k-1] of bit array.

INCREMENT(A)

1.     i < --- 0

2.     while i<k and A[i]=1

3.       do A[i] < --- 0 (flip, reset)

4.                               i < --- i+1

5.     if i<k

6.  then A[i] < ---  1  (flip, set)

Amortized (Aggregate) Analysis of INCREMENT (A)

The running time determined by #flips but not all bits flip each time INCREMENT is called. 

A[0] flips every time, total n times.

A[1] flips every other time, ën/2û times.

A[2] flips every forth time, ën/4û times.

….

for i=0,1,…,k-1, A[i] flips  ën/2ⁱû times.

Thus total #flips is

•         Thus the worst case running time is O(n) for a sequence of n INCREMENTs.

•         So the amortized cost per operation is O(1).