Binary Tree ADT: Implementation, Types, Application, Comparison

Binary Tree ADT

A binary tree is a tree in which no node can have more than two children. The maximum degree of any node is two. This means the degree of a binary tree is either zero or one or two.

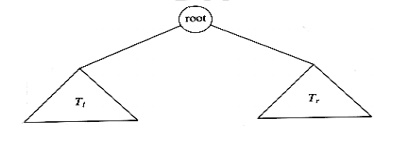
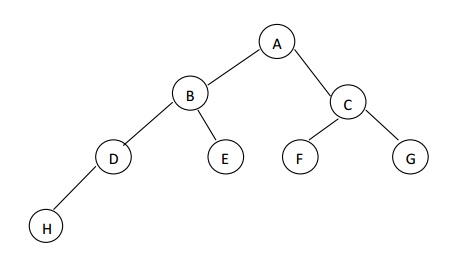
In the above fig., the binary tree consists of a root and two sub trees T_l & T_r. All nodes to the left of the binary tree are referred as left subtrees and all nodes to the right of a binary tree are referred to as right subtrees.

Implementation

A binary tree has at most two children; we can keep direct pointers to them. The declaration of tree nodes is similar in structure to that for doubly linked lists, in that a node is a structure consisting of the key information plus two pointers (left and right) to other nodes.

Binary Tree node declaration

typedef struct tree_node *tree_ptr; struct tree_node

{

element_type element;

tree_ptr left; tree_ptr right; };

typedef tree_ptr TREE;

Types of Binary Tree

i.           Strictly binary tree

Strictly binary tree is a binary tree where all the nodes will have either zero or two children. It does not have one child in any node.

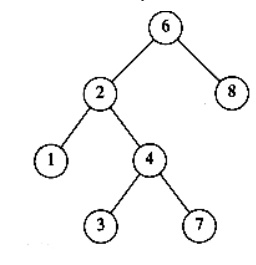
ii.    Skew tree

A skew tree is a binary tree in which every node except the leaf has only one child node. There are two types of skew tree, they are left skewed binary tree and right skewed binary tree.

Left skewed binary tree

A left skew tree has node with only the left child. It is a binary tree with only left subtrees.

Right skewed binary tree

A right skew tree has node with only the right child. It is a binary tree with only right subtrees.

iii.           Full binary tree or proper binary tree

A binary tree is a full binary tree if all leaves are at the same level and every non leaf node has exactly two children and it should contain maximum possible number of nodes in all levels. A full binary tree of height h has 2^h+1 – 1 nodes.

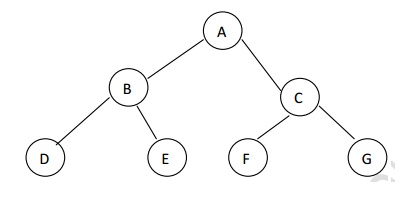
iv.    Complete binary tree

Every non leaf node has exactly two children but all leaves are not necessary at the same level. A complete binary tree is one where all levels have the maximum number of nodes except the last level. The last level elements should be filled from left to right.

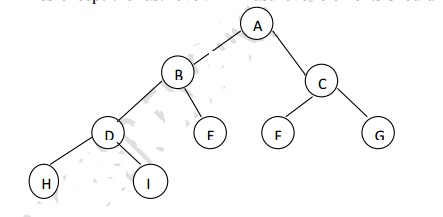
v.           Almost complete binary tree

An almost complete binary tree is a tree in which each node that has a right child also has a left child. Having a left child does not require a node to have a right child.

Comparison between General Tree and Binary Tree

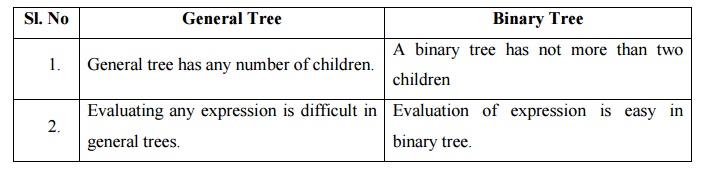
General Tree

1. General tree has any number of children.

2. Evaluating any expression is difficult in general trees.

Binary Tree

1. A binary tree has not more than two children

2. Evaluation of expression is easy in binary tree.

Application of trees

i.           Manipulation of arithmetic expression

ii.           Symbol table construction

iii.           Syntax Analysis

iv.          Grammar

v.           Expression Tree