Fibonacci Heaps

FIBONACCI HEAPS:

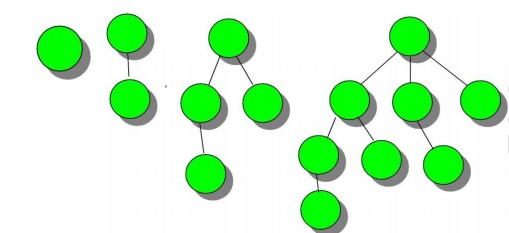
Binomial Tree:

A binomial tree of order 0 is a single node. A binomial tree of order k has a root of degree k and its children are roots of binomial trees of orders k-1, k-2, ..., 2, 1, 0 (in order). A binomial tree of order k has 2k nodes.

Data Structures:

·        Heap ordered Trees

·   Rooted, but unordered

·        Children of a node are linked together in a Circular, doubly linked List, E.g node 52

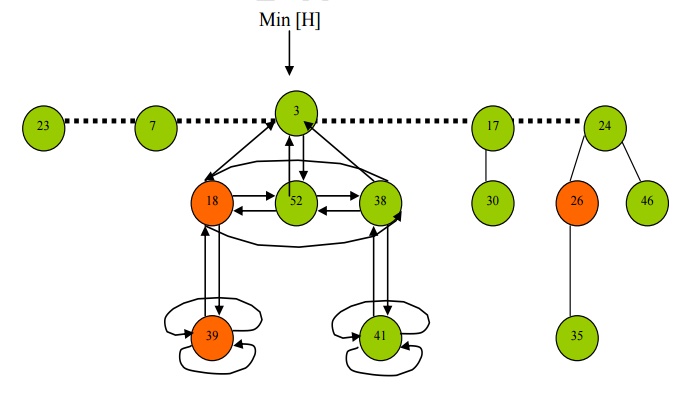
Node Pointers

-  left [x]

-  right [x]

-  degree [x]

-  number of children in the child list of x

-  mark [x]

Properties:

·        Collection of unordered Binomial Trees.

·        Support Mergeable heap operations such as Insert, Minimum, Extract Min, and Union in constant time O(1)

·        Desirable when the number of Extract Min and Delete operations is small relative to the number of other operations.

·        Most asymptotically fastest algorithms for computing minimum spanning trees and finding single source shortest paths make use of the Fibonacci heaps.

Fibonacci Heap Operations:

Make Fibonacci Heap

·        Assign N[H] = 0, min[H] = nil

·        Amortized cost is O(1)

Find Min

·        Access Min[H] in O(1) time

Uniting 2 Fibonacci Heaps

·        Concatenate the root lists of Heap1 and Heap2

·        Set the minimum node of the new Heap

·        Free the 2 heap objects

·        Amortized cost is equal to actual cost of O(1)

Insert

·        Amortized cost is O(1)

·        Initialize the structural fields of node x, add it to the root list of H

·        Update the pointer to the minimum node of H, min[H]

·        Increment the total number of nodes in the Heap, n[H]

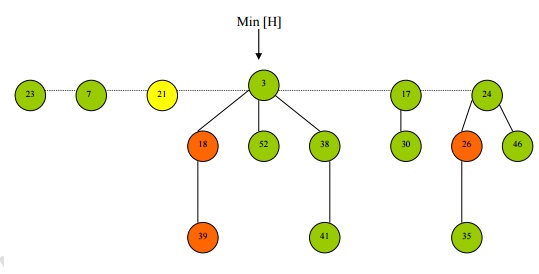
Example:

·   Node 21 has been inserted

·        Red Nodes are marked nodes – they will become relevant only in the delete operation.

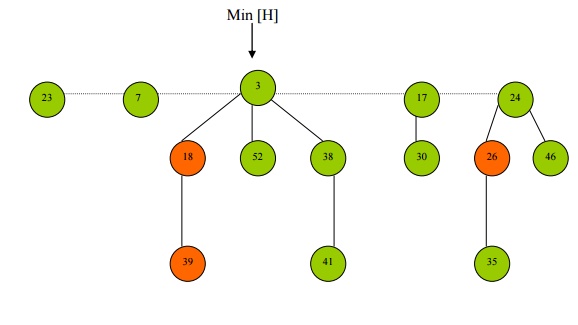
Extract Minimum Node

·        Amortized cost is O(D(n))

·        Make a root out of each of the minimum node‟s children.

·        Remove the minimum node from the root list, min ptr to right(x)

·        Consolidate the root list by linking roots of equal degree and key[x] <= key[y], until every root in the root list has a distinct degree value. (uses auxiliary array)

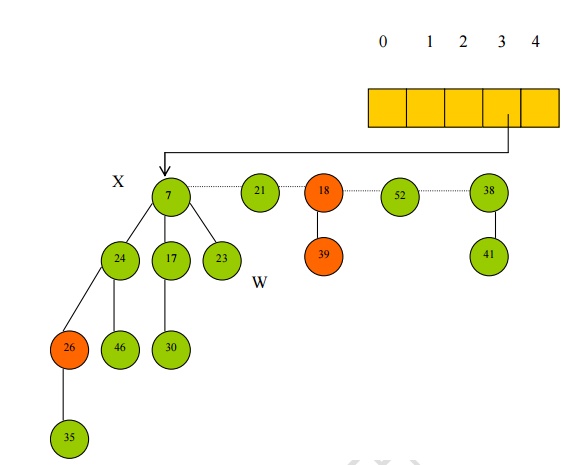
·        Root Nodes are stored in the auxiliary array in the index corresponding to their degree.

·        Hence node 7 is stored in index 3 and node 21 is stored in index 0.

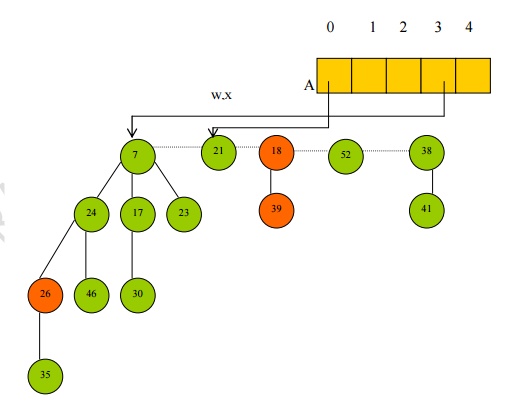
·        Further, node 18 is stored in index 1

·        There are no root nodes of index 2, so that array entry remains empty

·        Now the algorithm iterates through the auxiliary array and links roots of equal degree such that key[x] <= key[y],

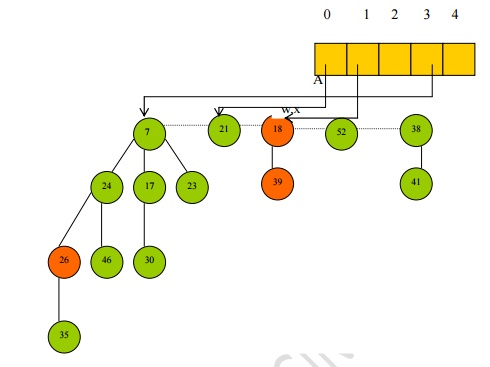
·        Nodes 21 and 52 are linked so that node 21 has degree 1, and it is then linked to node 18

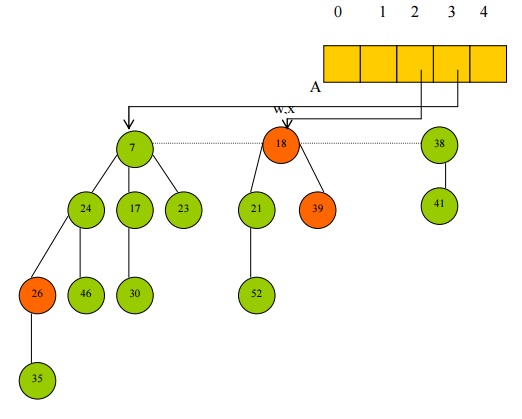
·        The pointers of the auxiliary array are updated.

·        But there are now no more remaining root nodes of duplicate degrees.

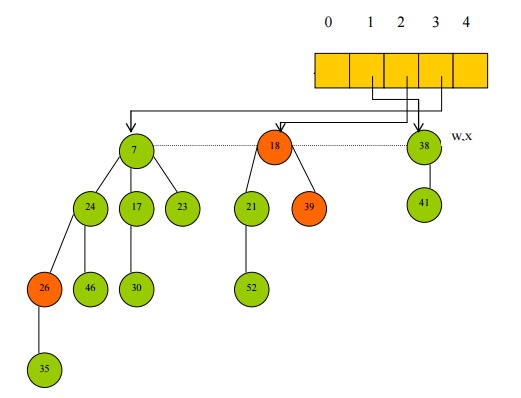
·   Extract-Min is now done.

·        The pointer min[H] is finally updated to the new minimum.

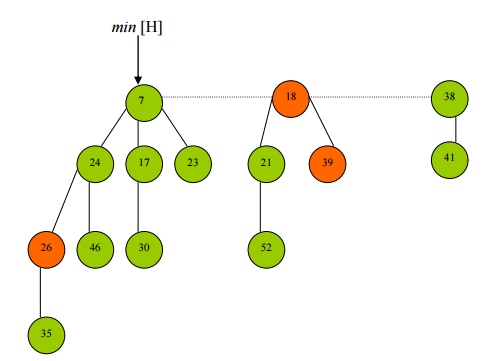
A node is marked if:

·        At some point it was a root then it was linked to anther node and 1 child of it has been cut.

·        Newly created nodes are always unmarked

·        A node becomes unmarked whenever it becomes the child of another node.

Decrease-Key

·        Amortized cost is O(1).

·        Check that new key is not greater than current key, then assign new key to x

·        If x is a root or if heap property is maintained, no structural changes

·        Else

o  Cut x: make x a root, remove link from parent y, clear marked field of x

o   Perform a Cascading cut on x‟s parent y (relevant if parent is marked):

§    if unmarked: mark y, return

§    if marked: Cut y, recurse on node y‟s parent

§    if y is a root, return

·        The Cascading cut procedure recurses its way up the tree until a root, or an unmarked node is found.

·        Update min[H] if necessary.

Example:

·        Suppose we want to decrease the keys of node 46  to 15.

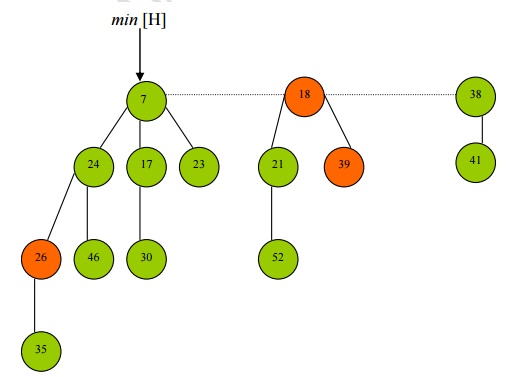
·        Since the new key of node 46 is 15 it violates the min-heap property, so it is cut and put on the root.

·        Suppose now we want to decrease the key of node 35 to 5.

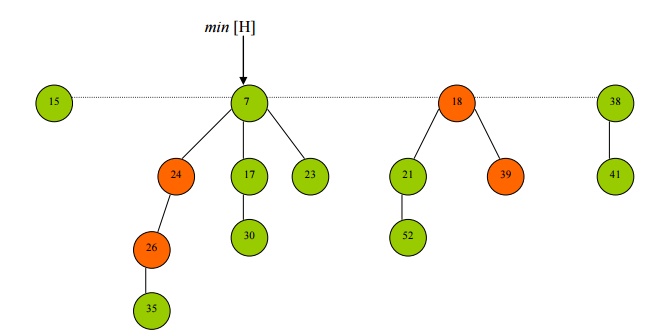
·        So node 5 is cut and place on the root list because again the heap property is violated.

·        But the parent of node 35, which is node 26, is marked, so we have to perform a

cascading cut.

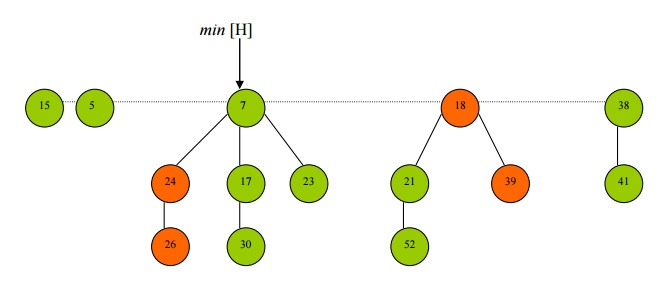
·        The cascading cut involves cutting the marked node, 26, unmarking it, and putting it on the root list.

·        We now repeat this procedure (recurse) on the marked nodes parent until we hit a node on the root list.

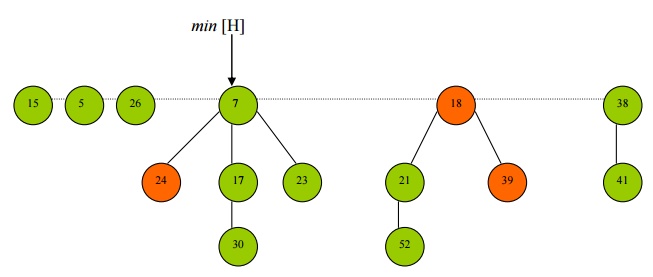
·        Since the next node encountered in the cascading cut procedure is a root node – node 7 – the procedure terminates.

·        Now the min heap pointer is updated.

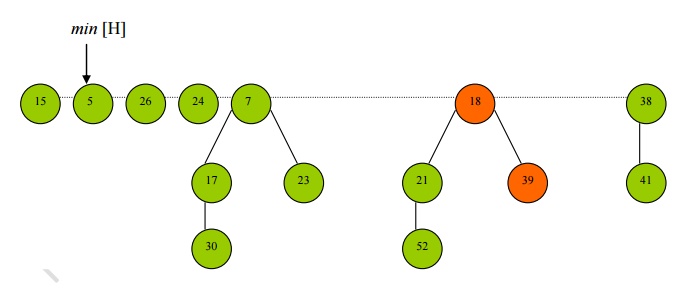
Delete-Key

·        Amortized cost is O(D(n))

·        Call Decease-Key on the node x that needs to be deleted in H, assigning negative infinity to it.

·        Call Extract-Min on H.