Red–black tree

RED-BLACK TREES

A red–black  tree is  a data  structure which  is  a  type  of self-balancing  binary  search  tree.

Balance is preserved by painting each node of the tree with one of two colors (typically called 'red' and 'black') in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be performed efficiently.

A binary search tree is a red-black tree if:

1. Every node is either red or black

2. Every leaf (nil) is black

3. If a node is red, then both its children are black

4.  Every simple path from a node to a descendant leaf contains the same number of black nodes

Black-height of a node x, bh(x), is the number of black nodes on any path from x to a leaf, not counting x

Inserting in Red-Black Tree

·        Color the node Red

·        Insert as in a regular BST

·        If have parent is red

Case 1

·                    x is node of interest, x's uncle is Red

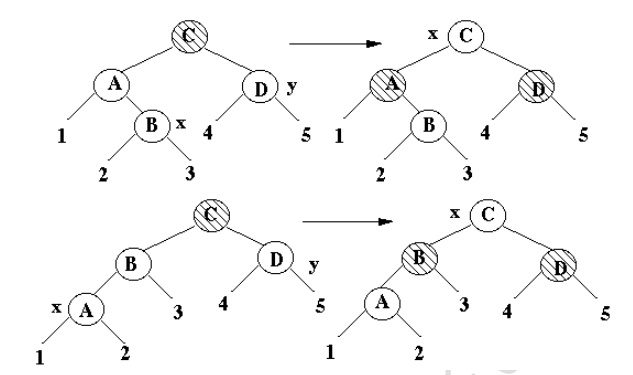
·   Decrease x's black height by one

Case 2

·        x's uncle is Black, x is a Right child

·        Transform to case 3

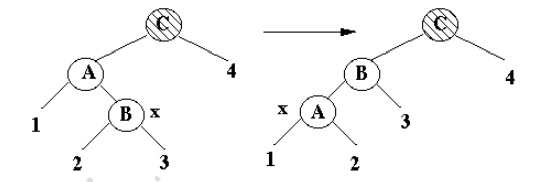
Case 3

·        x's uncle is Black, x is a Left child

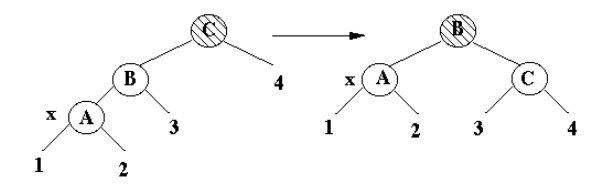
·        Terminal case, tree is Red-Black tree

·        Insertion takes O(lg(n)) time

·        Requires at most two rotations

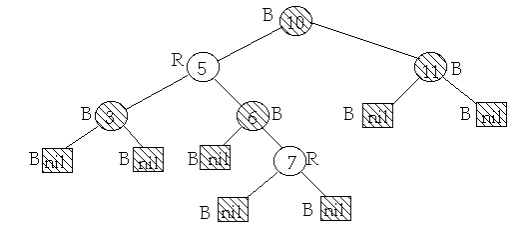
Example:

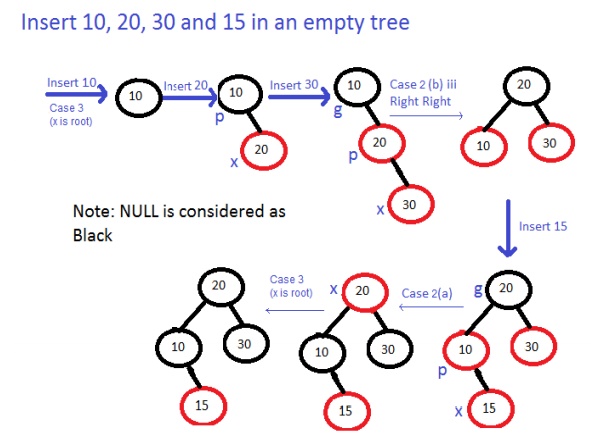
Deleting in a Red-Black Tree

·        Find node to delete

·        Delete node as in a regular BST

·        Node to be deleted will have at most one child

·        If we delete a Red node tree still is a Red-Black tree

·        Assume we delete a black node

·        Let x be the child of deleted node

·        If x is red, color it black and stop

·        If x is black mark it double black and apply the following:

Case 1

·        x's sibling is red

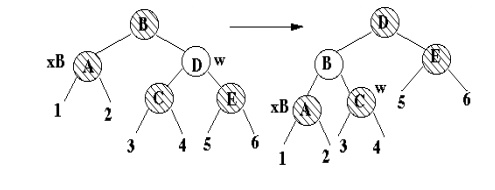
·        x stays at same black height. Transforms to case 2b then terminates.

Case 2a

·        x's sibling is black

·        x's parent is black

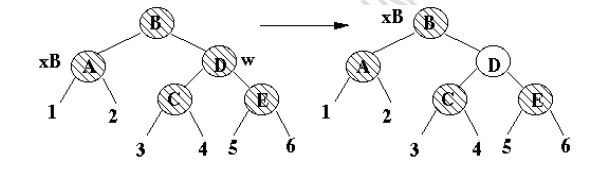
·        Decreases x black height by one

Case 2b

·        x's sibling is black

·        x's parent is red

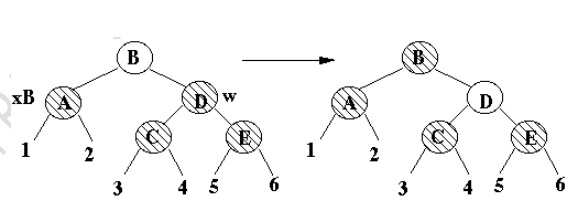
Terminal case, tree is Red-Black treep

Case 3

·        x's sibling is black

·        x's parent is either

·        x's sibling's left child is red

·        x's sibling's right child is black

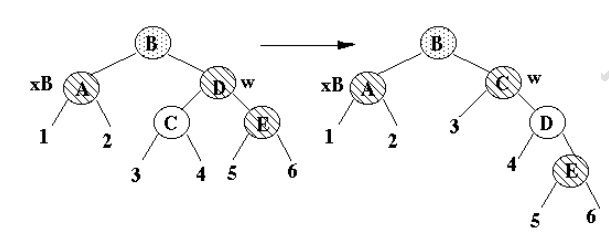
·   x stays at same black height

·        Transforms to case 4

Case 4

·        x's sibling is black

·        x's parent is either

·        x's sibling's left child is either

·        x's sibling's right child is red

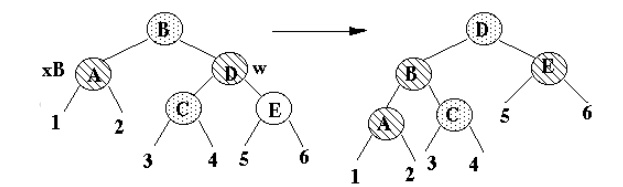
·        Terminal case, tree is Red-Black tree.

·        Delete time is O(lg(n)).

·        At most three rotations are done.