Binary search tree ADT

Binary search tree ADT

Binary search tree is a binary tree in which every node X in the tree, the values of all the keys in its left sub tree are smaller than the key value in X, and the values of all the keys in its right sub tree are larger than the key vale in X.

Comparison between binary tree and binary search tree

Binary tree

A tree is said to be a binary tree if it has atmost two children. It does not have any order.

Binary search tree

A binary search tree is a binary tree in which the key values in the left node is less than the root and the key values in the right node is greater than the root.

Declaration Routine for binary search tree

struct TreeNode;

typedef struct Treenode *SearchTree; SearchTree Insert (int X, SearchTree T); SearchTree Delete (int X, SearchTree T); int Find (int X, SearchTree T);

int FindMin(SearchTree T); int FindMax(SearchTree T);

SearchTree MakeEmpty(SearchTree T); struct TreeNode

{

int Element; SearchTree Left; SearchTree Right;

};

MakeEmpty

This operation is mainly for initialization when the programmer prefer to initialize the first element as a one node tree.

Routine to make an empty tree

SearchTree MakeEmpty(SearchTree T)

{

if (T!=NULL) {

MakeEmpty(T->Left);

MakeEmpty(T->Right); free(T);

}

return NULL;

}

Find

This operation requires returning a pointer to the node in tree T that has key X or NULL if there is no such node.

The find operation as follows.

^Ø   Check whether the root is NULL if so then return NULL.

^Ø   Otherwise, check the value X with the root node value (ie. T->Element)

^ü   If X is equal to T->Element, return T

^ü   If X is less than T->Element, traverse the left of T recursively.

^ü   If X is greater than T->Element, traverse the right of T recursively.

Routine for Find operation

Position Find( ElementType X, SearchTree T )

{

if( T == NULL ) return NULL;

if(X < T->element )

return( Find( X, T->left ) );

else

if( X > T->element )

return( Find( X, T->right ) );

else

return T;

}

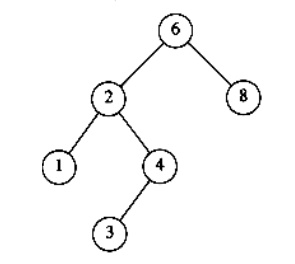
Example:

To find an element 4 (X = 4) in the below tree

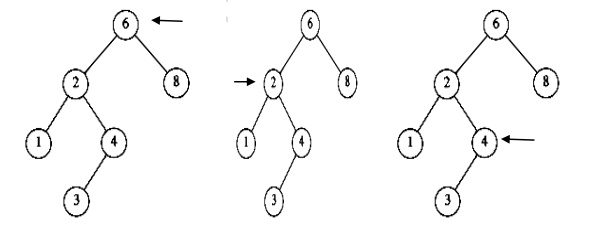
^Ø   In the first fig, the element 4 is checked with root 6. 4 is less than 6. So goto the left subtree.

^Ø   In the second fig, element 4 is checked with node 2. 4 is greater than 2. So goto the right subtree.

^Ø   In the third fig, the element 4 is checked with node 4. The element is equal. So return 4.

FindMin

This operation returns the position of the smallest element in the tree. To find the minimum element, start at the root and go left as long as there is a left child. The stopping point is the smallest element.

Recursive routine for FindMin

Position FindMin( SearchTree T )

{

if( T = = NULL ) return NULL;

else

if( T->Left = = NULL ) return T;

else

     return FindMin ( T->Left ) ; }

Non Recursive routine for FindMin

Position FindMin( SearchTree T )

{

if( T != NULL )

{

   while(T->Left!=NULL)

{

T = T->Left;

}}

return T; }

FindMax

This operation returns the position of the largest element in the tree. To find the maximum element, start at the root and go right as long as there is a right child. The stopping point is the largest element.

Insert

^Ø   To insert the element X in to the tree, check with the root node T.

^Ø   If it is less than the root, traverse the left sub tree recursively until it reaches the T->Left equals to NULL. Then X is placed in T->Left.

^Ø   If it is greater than the root, traverse the right sub tree recursively until it reaches the T->Right equals to NULL. Then X is placed in T->Right.

^Ø   If X is found in the tree, do nothing.

Recursive routine to insert an element into a binary search tree

SearchTree Insert( ElementType X, SearchTree T )

{

if( T = = NULL )

{ /* Create and return a one-node tree */

T = malloc ( sizeof (struct TreeNode) );

if( T != NULL )

{

T-Element = X;

T->Left = T->Right = NULL;

}

}

else

{

if( X < T->Element )

T->Left = Insert( X, T->Left ); else

if( X > T->Element )

T->Right = Insert( X, T->Right );

/* else X is in the tree already. We'll do nothing */

return T;

}

Example: To insert 8, 4, 1, 6, 5, 7, 10

i.        First insert element 8 which is considered as root.

ii.       Next insert element 4, 4 is less than 8, traverse towards left.

iii.      Next insert element 1, 1<8 traverse towards left. 1<4 traverse towards left.

iv.      To insert element 6, 6<8 traverse towards left. 6>4, place it as right child of 4.

v.       To insert element 5, 5<8 traverse towards left. 5>4, traverse towards right. 5<6, place it as left child of 6.

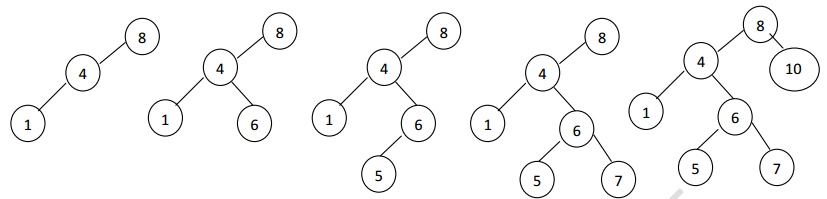
vi.          To insert element 7, 7<8 traverse towards left. 7>4, traverse towards right. 7>6, place it as right child of 6.

vii.    To insert element 10, 10>8, place it as a right child of 8.

Delete

While deleting a node from a tree, the memory is to be released. Deletion operation is the complex operation in the binary search tree. To delete a node from the tree consider the following three possibilities.

Case 1: Node to be deleted is a leaf node

Case 2: Node with one child.

Case 3: Node with two children.

Case 1: Deleting the leaf node

^Ø   Search the parent of the leaf node.

^Ø   Make the parent link of the leaf node as NULL.

^Ø   Release Memory.

Example: Deletion of node 6

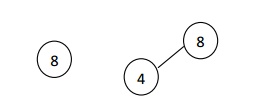
Case 2: Deleting the node with only one child.

^Ø   Search the parent of the node to be deleted.

^Ø   Assign the parent link to the child node of the node to be deleted.

^Ø   Release the memory of the deleted node.

If a node has one child, it can be deleted by adjusting its parent pointer to point to its child node.

Eg: Deletion of a node with one child, before and after

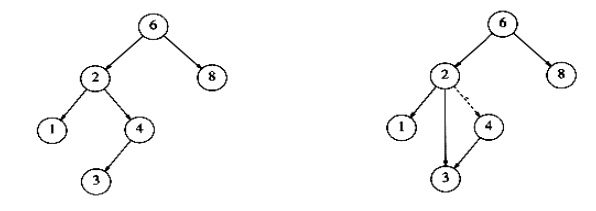
Case 3: Deleting a node with two children.

The general strategy is to replace the data of the node to be deleted with its smallest data of the right sub tree (or) largest data of the left sub tree and recursively delete the data or node.

Inorder to delete a node with two children, it can be replaced by a node whose key is larger than any node in P‟s right sub tree to preserve the Binary Search Tree property. The possible nodes that could replace node P are

Rule 1: The node with the largest value in P‟s left sub tree.

Rule 2: The node with the smallest value in P‟s right sub tree.

Eg: Deletion of a node 4 with two children, before and after

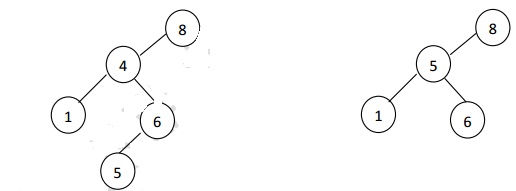
Deletion routine for binary search tree

SearchTree Delete( ElementType X, SearchTree T )

{

Position TmpCell;

if( T = = NULL )

Error("Element not found"); else

if( X < T->Element ) /* Go left */

T->Left = Delete( X, T->Left );

else

if( X > T->Element ) /* Go right */

T->Right = Delete( X, T->Right );

else    /* Found element to be deleted */

if( T->Left && T->Right ) /* Two children */

{ /* Replace with smallest in right subtree */

TmpCell = FindMin( T->Right );

T->Element = TmpCell->Element;

T->Right = Delete( T->Element, T->Right );

}

else    /* One or zero child */

{

TmpCell = T;      

if( T->Left = = NULL )  /* Only a right child */

T = T->Right;      

if( T->Right = = NULL )          /* Only a left child */

T = T->Left;        

free(TmpCell );    

}

return T;

}