Tree Introduction

TREE INTRODUCTION

Tree

A tree is a collection of nodes. The collection can be empty; otherwise a tree consists of a specially designed node called root, and one or more non empty sub trees T₁, T₂, …, T_k, each of whose roots are connected by a directed edge from root.

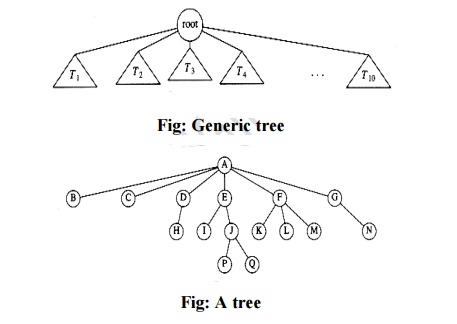
Root

The root is the first and top most nodes in the hierarchical arrangement of data items. A node which does not have a parent node is called root node. In the above tree, the root is A.

Node

Each data item present in the tree is called a node. It is the basic data structures that specifies the data information and have links to other data items. Example node A, B, …..,,

Q.

Leaf

A node which doesn‟t have children is called leaf or Terminal node. In the above tree B, C, H, I, K, L, M, N, P, Q are leaf node.

Siblings

Children of the same parents are said to be siblings. In the above tree B, C, D, E, F ,G are siblings, I,J are siblings, K, L, M are siblings, P, Q are siblings.

Path

A path from node n₁ to n_k is defined as a sequence of nodes n₁, n₂, . . . , n_k such that n_i is the parent of n_i+1 for 1 <= i <= k.

There is exactly only one path from the root to each node. In the above tree the path from A to P is A, E, J, P. Where A is the parent for E, E is the parent of J, and J is the parent of P.

Length

The length is defined as the number of edges on the path. The length for the path A to P is 3.

Degree

i.  Degree of a node

The number of sub trees of a node is called its degree. In the above tree, degree of A is 6, degree of F is 3, and degree of B is 0.

ii. Degree of a tree

The degree of the tree is the maximum degree of any node in the tree. In the above tree, the degree of the tree is 6.

Level

The level of a node is defined by initially letting the root be at level one. If a node is at level L then its children are at level L+1.

In the previous tree, the level of A is 1, level of B, C, D, E, F, G is 2, level of H, I, J, K, L, M, N is 3, and the level of P, Q is 4.

Depth

For any node n, the depth of n is the length of the unique path from root to n. For example, the depth of root A is 0, depth of c is 1, depth of H is 2, and the depth of P is 3

Height

For any node n, the heig ht of the node n is the length of the longest path from n to the leaf. The height of the leaf is zero. For example, the height of node F is 1, and the height of E is 2.

Note

^Ø    The height of the tree is equal to the height of the root.

^Ø    Depth of the tree is equal to the height of the tree.

Terminal node

A node with degree zero is called a terminal node. Leaf is called the terminal node because it has the degree 0. In the previous tree node B, C, H, I, K, L, M, N, P, Q are terminal nodes.

Non – Terminal Node

Any node whose degree is non zero is called Non – Terminal node. In the previous tree node A, D, E, F, G, J are non terminal nodes.

Edge

An edge is a condition line which connects two adjacent node of a tree. The line drawn from one node to another node is called edge. If a tree has N nodes, then there are N-1 edges. For example, the previous tree has 13 nodes and 12 edges.

Interior node

A node is said to be an interior node only if it is between root and leaves. All non terminal nodes except the root is called interior node. For example, D, E, F, G, J are interior nodes.

Ancestor node

A node is said to be an ancestor of another node only if it is the parent of that node or the parent of same ancestor of that node. For example, the ancestor of node H are A and D, and the ancestor of node F is A.

Descendent node

A node is said to be a descendent of another node if it is the child of that node or the child of some other descendent of that node. For example, the descendent of F are K, L, M, and the descendent of E are I, J, P, Q.

Forest

A forest is a set of disjoint trees. If the root is removed, then each node becomes a separate tree to become a forest.

Implementation of Trees

One way to implement a tree would be to have in each node, besides its data, a pointer to each child of the node. However, since the number of children per node can vary so greatly and is not known in advance, it might be infeasible to make the children direct links in the data structure, because there would be too much wasted space. The solution is simple: Keep the children of each node in a linked list of tree nodes.

typedef struct tree_node *tree_ptr;

struct tree_node

{

element_type element;

tree_ptr first_child;

tree_ptr next_sibling;

};

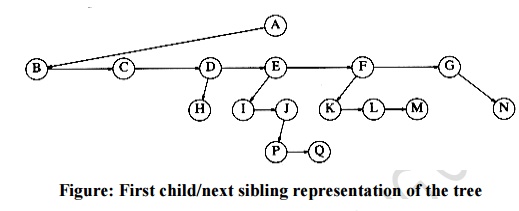
In the above fig, arrows that point downward are first_child pointers. Arrows that go left to right are next_sibling pointers.

Tree Traversals

Tree traversal is a method for visiting all the nodes in the tree exactly once. There are three types of tree traversal techniques, they are

i.           Inorder Traversal

ii.    Preorder Traversal

iii.           Postorder Traversal

Inorder Traversal

The inorder traversal of a binary tree is performed as

^Ø   Traverse the left subtree in inorder

^Ø   Visit the root

^Ø   Traverse the right subtree in inorder.

Recursive routine for inorder traversal

void inorder(Tree T)

{

if(T!=NULL)

{

inorder(T->left);

printElement(T->Element);

inorder(T->right);

}

}

Preorder Traversal

The preorder traversal of a binary tree is performed as

^Ø   Visit the root

^Ø   The left subtree in preorder

^Ø   Traverse the right subtree in preorder.

Recursive routine for preorder traversal

void preorder(Tree T)

{

if(T!=NULL)

{

printElement(T->Element);

preorder(T->left);

preorder(T->right);

}

}

Postorder Traversal

The postorder traversal of a binary tree is performed as

^Ø   Traverse the left subtree in postorder

^Ø   Traverse the right subtree in postorder.

^Ø   Visit the root

Recursive routine for postorder traversal

void postorder(Tree T)

{

if(T!=NULL)

{

postorder(T->left);

postorder(T->right);

printElement(T->Element);

}

}

Example

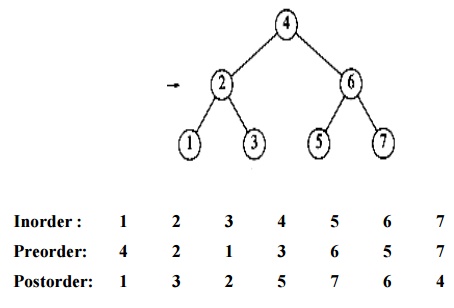
Inorder :      1        2        3        4        5        6        7

Preorder:     4        2        1        3        6        5        7

Postorder:   1        3        2        5        7        6        4