Splay trees

SPLAY TREES:

Splay trees are another variation of the binary search tree.

Novel characteristics:

·        Does not require any accounting information (color, level, height, etc.)

·        O(N) worst case for any single operation, but O(log N) average case

·        Frequently-accessed keys are moved up so that they are near the root.

Splay Operation:

Fundamental operation is the splay: this operation re-arranges the tree to make a specified node the root. A side-effect of the splay is that imbalances in the tree are corrected.

The simplest approach to splaying is the bottom-up approach, which is similar to the rebalancing operations we have seen for AVL, Red-Black, and AA-trees. On some path from a selected node back to the root, rotations are performed.

There are three cases for splaying. (Note that only the "left" cases are shown: there are symmetric "right" cases.)

·   Zig

·        Zig-Zig

·   Zig-Zag

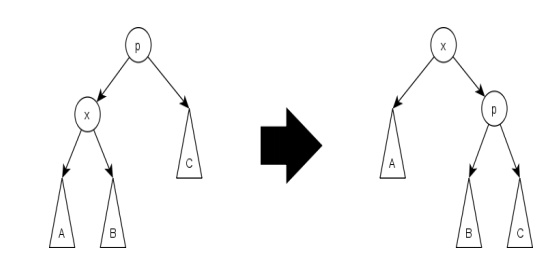
Zig Step:

This step is done when p is the root. The tree is rotated on the edge between x and p. Zig steps exist to deal with the parity issue and will be done only as the last step in a splay operation and only when x has odd depth at the beginning of the operation.

Zig-zig Step:

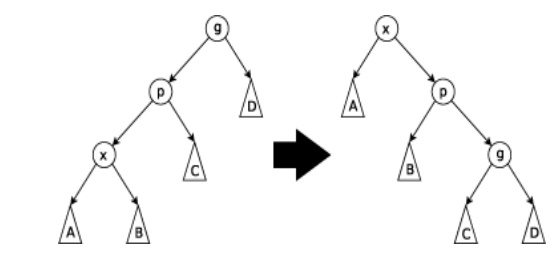
This step is done when p is not the root and x and p is either both right children or are both left children. The picture below shows the case where x and p are both left children. The tree is rotated on the edge joining p with its parent g, then rotated on the edge joining x with p.

Zig-zag Step:

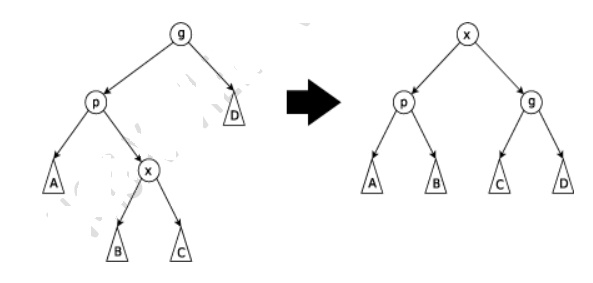
This step is done when p is not the root and x is a right child and p is a left child or vice versa. The tree is rotated on the edge between p and x, and then rotated on the resulting edge between x and g.

Overall splaying algorithm (bottom-up): splaying continues until the node X is the root of the overall tree.

A splay operation is performed after each access. We recursively apply the splaying strategy until the node of our interest reaches the root.

Example: Result of splaying at node 1 (after 1 is accessed).

·        Insertion: X is the newly inserted node (and will become the root after splaying).

·        Search:

o  If X is in the tree, X is the node found (and will become the root after

splaying).

o   If X is not in the tree, the last node accessed prior to reaching the NULL pointer is splayed.

·        Deletion:

o   First, X is the node to be deleted.  Splay it to the root (and delete it).

o  Then for the two subtrees L and R (left and right), we find the largest element in L. Splay it to the root of L. At this point, L's (new) root has no right child.

o  Finally connect R to the root of L as its right child.

Example: Delete 6