Chapter: Programming and Data structures : Advanced Non-Linear Data Structures
B-trees
B-TREES:
A B-tree
is a tree data structure that keeps data sorted and allows searches,
insertions, and deletions in logarithmic amortized time. Unlike self-balancing
binary search trees, it is optimized for systems that read and write large
blocks of data. It is most commonly used in database and file systems.
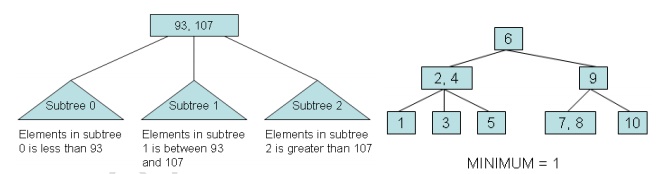
The B-Tree Rules
Important
properties of a B-tree:
·
B-tree nodes have many more than two children.
·
A B-tree node may contain more than just a single
element.
The set
formulation of the B-tree rules: Every B-tree depends on a positive constant
integer called MINIMUM, which is used to determine how many elements are held
in a single node.
·
Rule 1: The
root can have as few as one element (or even no elements if it also has no children); every other node has at
least MINIMUM elements.
·
Rule 2:
The maximum number
of elements in
a node is
twice the value
of
MINIMUM.
·
Rule 3: The
elements of each B-tree node are stored in a partially filled array, sorted from the smallest element (at index 0)
to the largest element (at the final used position of the array).
·
Rule 4: The
number of subtrees below a nonleaf node is always one more than the
number of
elements in the node.
o Subtree 0, subtree 1, ...
·
Rule 5: For any
nonleaf node:
1.
An element at index i is greater than all the elements in subtree number i of the node, and
2. An element at index i is less than all the elements in subtree number i + 1 of the node.
Rule 6: Every leaf in a B-tree has the same depth. Thus it ensures that a B-tree avoids the problem of a unbalanced tree.
The Set Class Implementation with B-Trees
"Every child of a node is also the root of a
smaller B-tree".
public
class IntBalancedSet implements Cloneable
{
private
static final int MINIMUM = 200;
private
static final int MAXIMUM = 2*MINIMUM;
int
dataCount;
int[]
data = new int[MAXIMUM + 1];
int
childCount;
IntBalancedSet[]
subset = new IntBalancedSet[MAXIMUM + 2];
// Constructor:
initialize an empty set public IntBalancedSet()
// add: add
a new element to this set, if the element was already in the set, then there is
no change.
public
void add(int element)
// clone:
generate a copy of this set.
public
IntBalancedSet clone()
//
contains: determine whether a particular element is in this set
pubic
boolean contains(int target)
//
remove: remove a specified element from this set
public
boolean remove(int target)
}
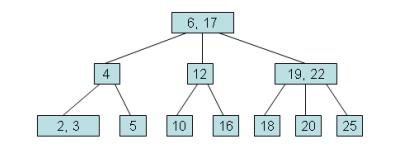
Searching for a Target in a Set
The
psuedocode:
1. Make a
local variable, i, equal to the first
index such that data[i] >= target.
If there is no such index, then set i
equal to dataCount, indicating that none of the elements is greater than or
equal to the target.
2. if (we
found the target at data[i]) return
true;
else if
(the root has no children) return false;
else
return subset[i].contains(target);
Example, try to search for 10.
We can
implement a private method:
private
int firstGE(int target), which returns the first location in the root such that
data[x] >= target. If there's no
such location, then return value is dataCount.
Adding an Element to a B-Tree
It is
easier to add a new element to a B-tree if we relax one of the B-tree rules.
Loose
addition allows the root node of the B-tree to have MAXIMUM = 1 elements. For
example, suppose we want to add 18 to the tree:
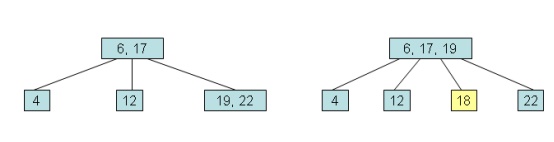
The above
result is an illegal B-tree. Our plan is to perform a loose addition first, and
then fix the root's problem.
The Loose Addition Operation for
a B-Tree:
private
void looseAdd(int element)
{
i =
firstGE(element) // find the first index such that data[i] >= element
if (we
found the new element at data[i]) return; // since there's already a copy in
the set else if (the root has no children)
Add the
new element to the root at data[i]. (shift array)
else {
subset[i].looseAdd(element);
if the
root of subset[i] now has an excess element, then fix that problem before
returning.
}
}

private
void fixExcess(int i)
// precondition:
(i < childCount) and the entire B-tree is valid except that subset[i] has
MAXIMUM + 1 elements.
//postcondition:
the tree is rearranged to satisfy the loose addition rule
Fixing a Child with an Excess
Element:
·
To fix a child with MAXIMIM + 1 elements, the child
node is split into two nodes that each contain MINIMUM elements. This leaves
one extra element, which is passed up to the parent.
·
It is always the middle element of the split node
that moves upward.
·
The parent of the split node gains one additional
child and one additional element.
· The children of the split node have been equally distributed between the two smaller nodes.
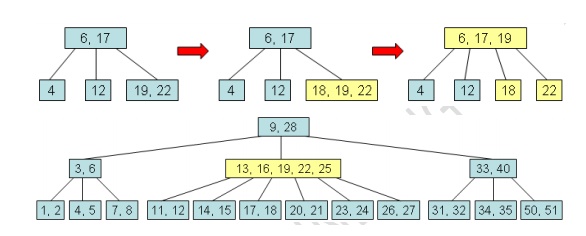
Fixing the Root with an Excess
Element:
·
Create a new root.
·
fixExcess(0).
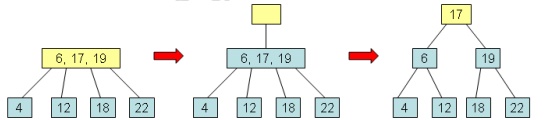
Removing an Element from a B-Tree
Loose removal rule: Loose
removal allows to leave a root that has one element too few. public boolean remove(int target)
{
answer =
looseRemove(target);
if
((dataCount == 0) && (childCount == 1))
Fix the
root of the entire tree so that it no longer has zero elements;
return
answer;
}
private
boolean looseRemove(int target)
{
1. i =
firstGE(target)
2. Deal with
one of these four possibilities:
2a. if
(root has no children and target not found) return false.
2b. if(
root has no children but target found) {
remove
the target
return
true
}
2c. if (root has children and target not found)
{ answer = subset[i].looseRemove(target)
if (subset[i].dataCount < MINIMUM)
fixShortage(i) return true
}
2d. if (root has children and target found) {
data[i] = subset[i].removeBiggest()
if (subset[i].dataCount < MINIMUM)
fixShortage(i)
return
true
}
}
private
void fixShortage(int i)
// Precondition:
(i < childCount) and the entire B-tree is valid except that subset[i] has
MINIMUM - 1 elements.
// Postcondition:
problem fixed based on the looseRemoval rule.
private
int removeBiggest()
// Precondition:
(dataCount > 0) and this entire B-tree is valid
// Postcondition:
the largest element in this set has been removed and returned. The entire
B-tree is still valid based on the looseRemoval rule.
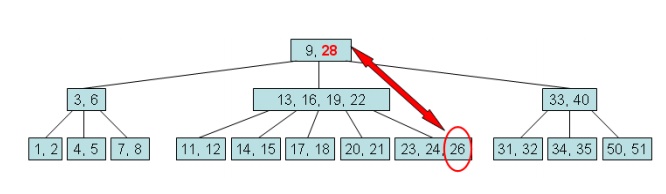
Fixing Shortage in a Child:
When
fixShortage(i) is activated, we know
that subset[i] has MINIMUM - 1
elements. There are four cases that we need to consider:
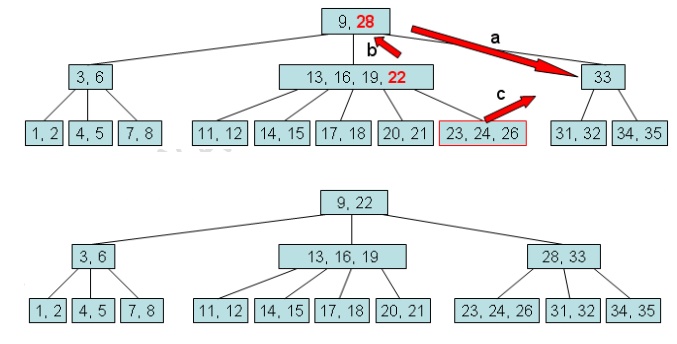
Case 1: Transfer an extra element from
subset[i-1]. Suppose subset[i-1] has more than the MINIMUM number of elements.
a. Transfer
data[i-1] down to the front of
subset[i].data.
b. Transfer
the final element of subset[i-1].data
up to replace data[i-1].
c. If
subset[i-1] has children, transfer
the final child of subset[i-1] over
to the front of subset[i].
Case 2: Transfer an extra element from
subset[i+1]. Suppose subset[i+1] has more than the MINIMUM number of elements.
Case 3: Combine subset[i] with
subset[i-1]. Suppose subset[i-1] has only MINIMUM elements
a. Transfer
data[i-1] down to the end of subset[i-1].data.
b. Transfer
all the elements and children from subset[i]
to the end of subset[i-1].
c. Disconnect
the node subset[i] from the B-tree by
shifting subset[i+1], subset[i+2] and so on leftward.
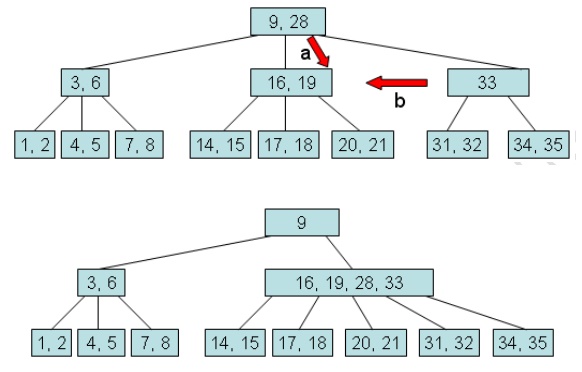
Case 4: Combine subset[i] with
subset[i+1]. Suppose subset[i+1] has only MINIMUM
elements.
We may need to continue activating fixShortage() until the B-Tree rules are
satisfied.
Removing the Biggest Element from
a B-Tree:
private
int removeBiggest()
{
if (root
has no children)
remove and return the last element else {
answer =
subset[childCount-1].removeBiggest() if (subset[childCount-1].dataCount <
MINIMUM)
fixShortage(childCount-1) return answer
}
}
A more concrete example for node
deletion:
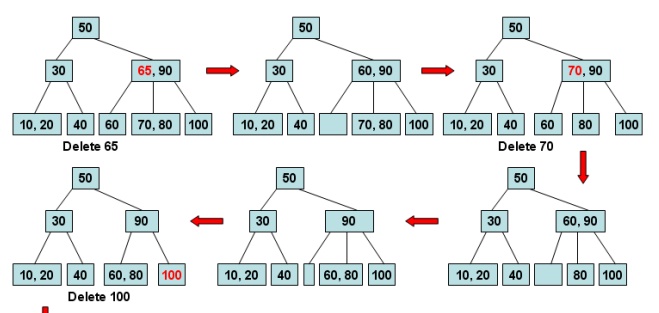

Related Topics