AVL Trees

AVL TREES:

An AVL (Adelson – Velskii and Landis) tree is a binary search tree with a balance condition. A balance factor is the height of the left sub tree minus height of the right sub tree. The height of the empty tree is defined to be -1. For an AVL tree all balance factor should be +1, 0, or -1.

If the balance factor of any node in an AVL tree becomes less than -1 or greater than 1, the tree has to be balanced by making a simple modifications in the tree called rotation.

An AVL tree causes imbalance, when any one of the following conditions occur. α – is the node must be rebalanced.

Case 1: An insertion from the left sub tree of the left child of node α.

Case 2: An insertion into the right sub tree of the left child of α.

Case 3: An insertion into the left sub tree of the right child of α.

Case 4: An insertion into the right sub tree of the right child of α.

These imbalances can be overcome by

i.            Single Rotation

ii.           Double Rotation

Case 1 and Case 4 imbalance (left – left or right – right) is fixed by a single rotation of the tree. Case 2 and Case 3 imbalance (left – right or right – left) is fixed by double rotation.

Single Rotation

Single rotation with left

The following fig. shows the single rotation that fixes case 1. 

General Representation

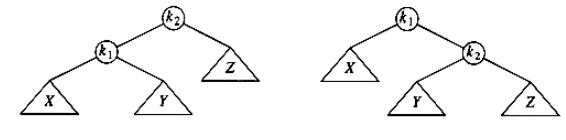
The before picture is on the left, and the after is on the right. Node K₂ violates the AVL property because its left sub tree is two levels deeper than its right sub tree. Sub tree X has grown to an extra level, causing it to be exactly two levels deeper than Z. To ideally rebalance the tree, we would like to move X up a level and Z down a level. To do this we rearrange nodes into an equivalent tree as shown in the second part of the above fig.

Eg: If we insert the value 1 in the left sub tree of the following tree it causes imblance

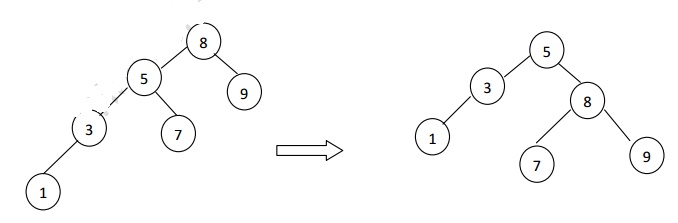
The above fig. shows that after the insertion of 1 into the original AVL tree on the left, node 8 becomes unbalanced. Thus we do a single rotation between 5 and 8, obtaining tree on the right.

Routine to perform single rotation with left

static Position SingleRotateWithLeft ( Position K2 )

{

Position K1;

K1 = K2->Left;

K2->Left = K1->Right;

K1->Right = K2;

K2->Height = Max ( Height (K2 ->Left), Height(K2->Right))+1;

K1->Height = Max ( Height (K1 ->Left), Height(K1->Right))+1;

return K1;

}

Single rotation with right

General Representation

Routine to perform single rotation with right

static Position SingleRotateWithRight ( Position K1 )

{

Position K2;

K2 = K1->Right;

K1->Right = K2->Left;

K2->Left = K1;

K2->Height = Max ( Height (K2 ->Left), Height(K2->Right))+1;

K1->Height = Max ( Height (K1 ->Left), Height(K1->Right))+1;

return K2;

}

Example

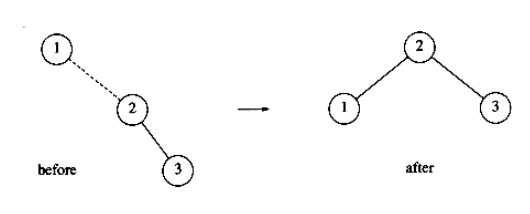
Suppose we start with an initially empty AVL tree and insert the keys 1 through 7 in sequential order. The first problem occurs when it is time to insert key 3, because the AVL property is violated at the root. We perform a single rotation between the root and its right child to fix the problem. The tree is shown in the following figure, before and after the rotation:

Next, we insert the key 4, which causes no problems, but the insertion of 5 creates a violation at node 3, which is fixed by a single rotation. Besides the local change caused by the rotation, the programmer must remember that the rest of the tree must be informed of this change. Here, this means that 2's right child must be reset to point to 4 instead of 3.

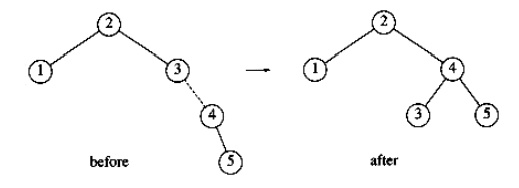
Next, we insert 6. This causes a balance problem for the root, since its left subtree is of height 0, and its right subtree would be height 2. Therefore, we perform a single rotation at the root between 2 and 4.

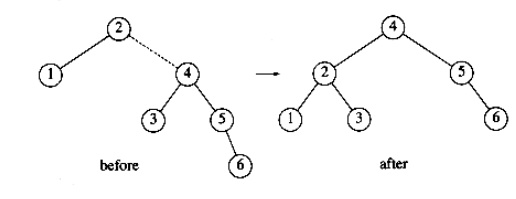
The rotation is performed by making 2 a child of 4 and making 4's original left sub tree the new right sub tree of 2. Every key in this sub tree must be positioned between 2 and 4, so this transformation makes sense. The next key we insert is 7, which causes another rotation.

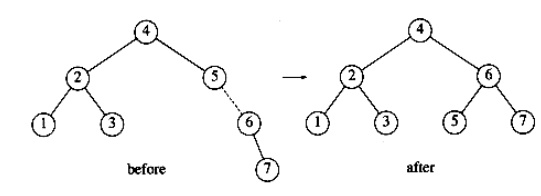
Double Rotation

Double Rotation with left

Double rotation with left is used to perform case 2. An insertion into the right sub tree of the left child of node α.

Double Rotation with left is performed by first performing single rotation with right, and then performing single rotation with left.

Routine to perform double rotation with left

static Position DoubleRotateWithLeft( Position K3)

{

/* Rotate between K1 and K2 */

K3 -> Left = SingleRotateWithRight(K3 ->Left); /* Rotate between K3 and K2 */

return SingleRotateWithLeft (K3);

}

Double Rotation with Right

Double rotation with right is used to perform case 4. An insertion into the left sub tree of the right child of node α.

Double Rotation with right is performed by first performing single rotation with left, and then performing single rotation with right.

Routine to perform double rotation with right

static Position DoubleRotateWithRight( Position K1)

{

K1 -> Right = SingleRotateWithLeft(K1 ->Right);

return SingleRotateWithRight (K1);

}

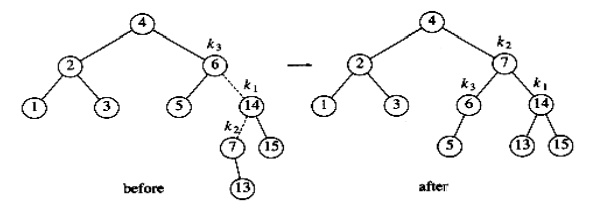
In our example, the double rotation is a right-left double rotation and involves 7, 15, and 14. Here, k₃ is the node with key 7, k₁ is the node with key 15, and k₂ is the node with key 14.

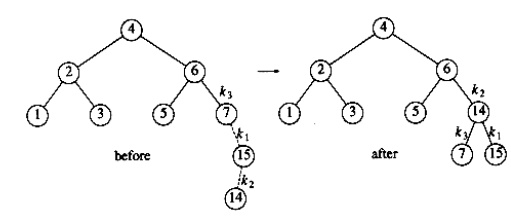
Next we insert 13, which require a double rotation. Here the double rotation is again a right-left double rotation that will involve 6, 14, and 7 and will restore the tree. In this case, k₃ is the node with key 6, k₁ is the node with key 14, and k₂ is the node with key 7.

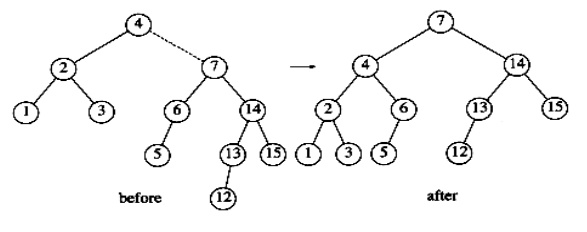
If 12 is now inserted, there is an imbalance at the root. Since 12 is not between 4 and 7, we know that the single rotation will work.

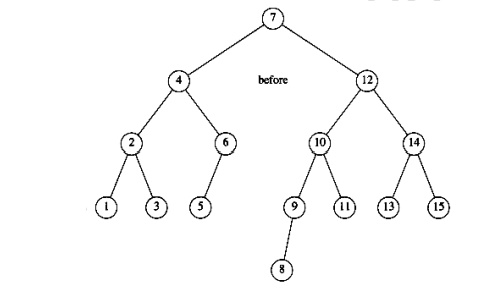
Insertion of 11 will require a single rotation:

To insert 10, a single rotation needs to be performed, and the same is true for the subsequent insertion of 9. We insert 8 without a rotation, creating the almost perfectly balanced tree that follows.

Node declaration for AVL trees

#ifndef _AvlTree_H struct AvlNode;

typedef struct AvlNode *Position;

typedef struct AvlNode *AvlTree;

AvlTree MakeEmpty(AvlTree T);

Position Find( ElementType X, AvlTree T);

Position FindMin( AvlTree T);

Position FindMax( AvlTree T);

AvlTree Insert( ElementType X, AvlTree T);

AvlTree Delete( ElementType X, AvlTree T);

ElementType Retrieve( Position P); #endif

struct AvlNode

{

ElementType Element;

AvlTree Left;

AvlTree Right;

int Height;

};

Function to compute height of an Avl node

static int Height( Position P)

{

if( P = = NULL) return -1;

else

return P -> Height;

}

Insertion into an Avl tree

AvlTree Insert( ElementType X, AvlTree T)

{

if( T = = NULL)

{

T = malloc( sizeof( struct AvlNode));

if( T = = NULL)

FatalError( “ Out of Space”);

else

{

T -> Element = X;

T -> Height = 0;

T -> Left = T -> Right = NULL;

}

}

else if( X < T -> Element)

{

T -> Left = Insert(X, T-> Left);

if( Height( T -> Left) – Height( T -> Right) = = 2)

if( X < T -> Left -> Element)

T = SingleRotateWithLeft( T );

else

T = DoubleRotateWithLeft(T);

}

else if( X > T -> Element)

{

T -> Right = Insert(X, T-> Right);

if( Height( T -> Right) – Height( T -> Left) = = 2) if( X > T -> Right -> Element)

T = SingleRotateWithRight( T );

else

T = DoubleRotateWithRight(T);

}

/* Else X is in the tree already; we will do nothing */

T -> Height = Max( Height( T-> Left), Height( T -> Right)) + 1;

return T;

}