Disjoint Sets data structure

DISJOINT SETS:

A disjoint sets data structure represents a collection of sets that are disjoint: that is, no item is found in more than one set. The collection of disjoint sets is called a partition, because the items are partitioned among the sets. A disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non overlapping) subsets.

The Disjoint Set data structure solves a specific problem that is interesting both theoretically and practically. The problem is as follows:

You have a collection of n items, which you number from 0 to n-1. These items will be partitioned into some number of sets. The sets are "disjoint" which means that no item belongs to more than one set. All items belong to some set though (hence the use of the word "partition.").

There are two operations that you can perform:

·        int Find(i): This takes the number of an item and returns its "set id." This is a number

between zero and n-1. You don't really care what the number is; however, if i and j belong to the same disjoint set, then Find(i) will equal Find(j).

int Disjoint::Find(int element)

{

while (links[element] != -1) element = links[element]; return element;

}    

·        int Union(id1, id2): This takes the set id's of two different sets, and performs the union operation on them, coalescing them into one set. It returns the set id of this new set. Now, when you call Find() on any item that was previously in either of these sets, it will return this new set id.

int Disjoint::Union(int s1, int s2)

{

int p, c;

if (links[s1] != -1 || links[s2] != -1) {

cerr << "Must call union on a set, and not just an element.\n";

exit(1);

}

if (ranks[s1] > ranks[s2])

{

p = s1; c = s2;

}

else

{

p = s2; c = s1;

}

links[c] = p;

ranks[p] += ranks[c]; /* HERE */ return p;

}

Abstract implementation

In the abstract, we implement disjoint sets with circles and arrows, which we'll call "nodes" and links. Each element will be in its own node, and each element has one link. That link is either to another node, or to NULL. In the beginning, when you first set up an instance of disjoint sets, all nodes will have NULL links.

When a node has a NULL link, we call it the "root" of a set. If you call Find() on a node with a NULL link, it will return the node's item number, and that is the set id of the node. Therefore, when you first start, every node is the root of its own set, and when you call Find(i), it will return i.

When you call Union(i, j), remember that i and j must be set id's. Therefore, they must be nodes with NULL links. What you do is have one of those nodes set its link to the other node.

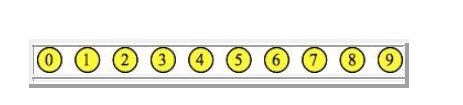
Example:

We initialize an instance of disjoint sets with 10 items. Each item is a node with a number from 0 to 9. Each node has a NULL link, which we depict by not drawing any arrows from the node:

Again, each node is in its own set, and each node's set id is its number. Suppose we call Union(0, 1), Union(2, 3) and Union(4, 5). These will each set one of the node's link to the other node. We'll talk about how that gets done later. However, suppose this is the result:

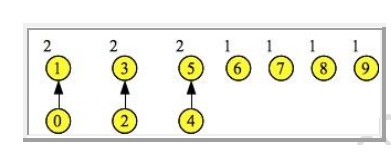
Node 0's link has been set to 1. Both of these nodes' set ids are now 1, which means Find(0) equals Find(1) equals one. Similarly, Find(2) equalsFind(3) equals three. This gives you a clue about implementing Find(). When you call Find(n), what you do is keep setting n to n's link, until n's link is NULL. At that point, you are at the root of the set, and you return n.

Union is pretty simple, too, but you have some choices about how to determine which node sets its link field to the other. We use three methods to do this:

1.     Union by size: Make the node whose set size is smaller point to the node whose set size is bigger. Break ties arbitrarily.

2.     Union by height: The height of a set is the longest number of links that it takes to get from one of its items to the root. With union by height, you make the node whose height is smaller point to the node whose height is bigger.

3.     Union by rank with path compression: This works exactly like union by height, except you don't really know the height of the set. Instead, you use the set's rank, which is what its height would be, were you using union by height. The reason that you don't know the height is that when you call Find(i) on an element, you perform "path compression."

 There are two sets, with set id's 5 and 9. Now, suppose you call Find(0). It will return five, but along the way to the root node of its set, it encounters nodes 1 and 3. Before returning five, it sets the links to 0, 1 and 3 to five:

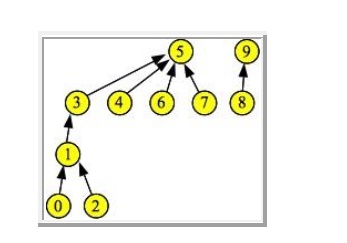
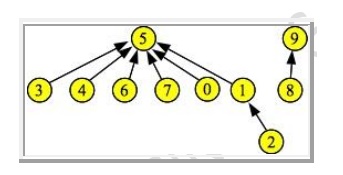
Running Time:

We assume the number of items in the instance of disjoint sets is n:

·        Initializing an instance of disjoint sets: O(n)

·        Performing Union() in any of the implementations: O(1)

·        Performing Find() in Union by size or height: O(log(n))

·        Performing Find() in Union by rank with path compression: O(α(n))