Representation of Graphs

REPRESENTATION OF GRAPHS:

Graph

A graph G = (V, E) consists of a set of vertices, V, and a set of edges, E. Vertices are referred to as nodes. The arcs between the nodes are referred to as edges. Each edge is a pair (v,w), where v,w € V. Edges are sometimes referred to as arcs.

In the above graph V₁, V₂, V₃, V₄ are the vertices and (V₁, V₂), (V₂, V₃), (V₃, V₄), (V₄, V₁), (V₁, V₃), (V₂, V₄) are the edges.

Directed Graph (or) Digraph

Directed graph is a graph, which consists of directed edges, where each edge in E is unidirectional. In directed graph, the edges are directed or one way. it is also called as digraphs. If (v,w) is a directed edge, then (v,w) ≠ (w,v).

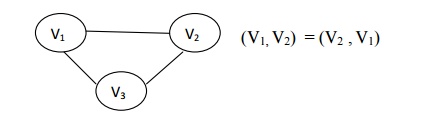
Undirected Graph

An undirected graph is a graph, which consists of undirected edges. In undirected graph, the edges are undirected or two way. If (v,w) is a undirected edge, then (v,w) = (w,v).

Weighted Graph

A graph is said to be weighted graph if every edge in the graph is assigned a weight or value. It can be directed or undirected.

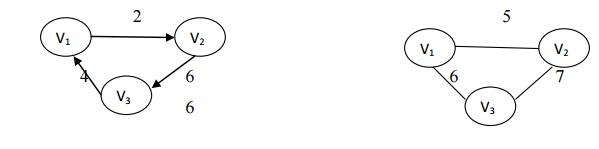
Subgraph

A subgraph of a graph G = (V,E) is a graph G` = (V`, E‟) such that V` V and E‟ E.

Symmetric digraph

A symmetric digraph is a directed graph such that for every edge vw there is also a

reverse edge wv.

Symmetric undirected graph

Every  undirected  graph  is  a  symmetric  digraph  where  each  undirected  edge  is  considered as a pair of directed edges in opposite direction.

Complete Graph

A complete graph is a graph in which there is an edge between every pair of vertices.

A complete graph with n vertices will have n(n-1)/2.

A complete graph is a strongly connected graph.

Strongly connected Graph

If there is a path from every vertex to every other vertex in a directed graph then it is said to be strongly connected graph. Otherwise, it is said to be weakly connected graph.

Path

A path in a graph is defined as a sequence of verices w₁, w₂, w₃, . . . , w_n such that (w₁, w₂, w₃, . . .) € E. Where E is the number of edges in a graph. Path from A to D is {A, B, C, D} or {A, C, D}

Path from A to C is {A, B, C} or {A, C}

Length

The length of a path in a graph is the number of edges on the path, which is equal to N–1. Where N is the number of vertices.

Length of the path from A to B is {A, B} = 1

Length of the path from A to C is {A, C} = 1 & {A, B, C} = 2.

If there is a path from a vertex to itself with no edges then the path length is 0. Length of the path from A->A & B -> B is 0.

Loop

A loop in a graph is defined as the path from a vertex to itself. If the graph contains an edge (v,v) from a vertex to itself, then the path v, v is sometimes referred to as a loop.

Simple Path

A simple path is a path such that all vertices are distinct (different), except that the first and last vertexes are same.

Simple path for the above graph {A, B, C, D, A}. First and Last vertex are the same ie. A

Cycle

A cycle in a graph is a path in which the first and the last vertex are the same.

Cyclic Graph

A graph which has cycles is referred to as cyclic graph. A graph is said to be cyclic, if the edges in the graph should form a cycle.

Acyclic Graph

A graph is said to be acyclic, if the edges in the graph does not form a cycle.

Directed Acyclic Graph (DAG)

A directed graph is acyclic if it has no cycles, and such types of graph is called as Directed Acyclic Graph.

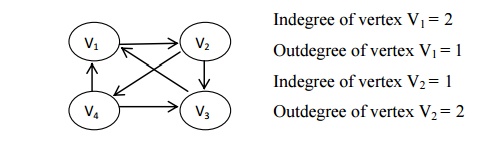
Degree

The number of edges incident on a vertex determines its degree. The degree of the vertex V is written as degree (V).

Indegree : The indegree of the vertex V, is the number of edges entering into the vertex V.

Outdegree: The outdegree of the vertex V, is the number of edges exiting from the vertex V.

Representation of Graph

A Graph can be represented in two ways.

i.           Adjacency Matrix

ii.    Adjacency List

Adjacency Matrix Representation

i.           Adjacency matrix for directed graph

ii.           Adjacency matrix for undirected graph

iii.           Adjacency matrix for weighted graph

Adjacency matrix for directed graph

One simple way to represent a graph is Adjacency matrix. The adjacency matrix A for a graph G = (V, E) with n vertices is an n x n matrix, such that

A_ij = 1, if there is an edge V_i to V_j A_ij = 0, if there is no edge

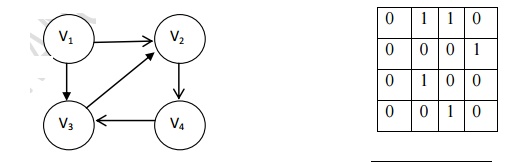
Adjacency matrix for undirected graph 

Adjacency matrix for weighted graph

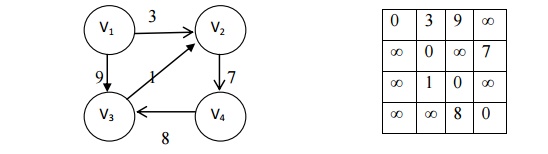
Here A_ij = C_ij if there exists an edge from V_i to V_j. (C_ij is the weight or cost). A_ij = 0, if there is no edge.

If there is no arc from i to j, C[i,j] = ∞, where i ≠ j.

Advantage

^Ø   Simple to implement.

Disadvantage

^Ø   Takes O(n²) space to represents the graph.

^Ø   Takes O(n²) time to solve most of the problem.

Adjacency List Representation

In this representation, we store the graph as a linked structure. We store all vertices in a list and then for each vertex, we have a linked list of its adjacency vertices.

Adjacency List for directed unweighted graph

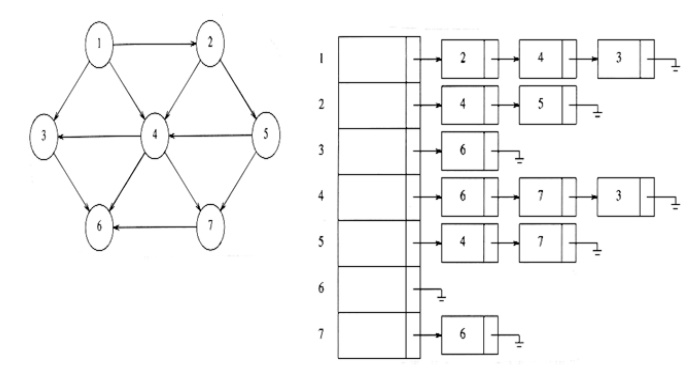
Disadvantage of Adjacency list representation

It takes O(n) time to determine whether there is an arc from vertex i to vertex j, since there can be O(n) vertices on the adjacency list for vertex i.