Floyd - Warshall Algorithm

FLOYD - WARSHALL ALGORITHM:

The Floyd-Warshall algorithm works based on a property of intermediate vertices of a shortest path. An intermediate vertex for a path p = <v₁, v₂, ..., v_j> is any vertex other than v₁ or v_j.

If the vertices of a graph G are indexed by {1, 2, ..., n}, then consider a subset of vertices {1, 2, ..., k}. Assume p is a minimum weight path from vertex i to vertex j whose intermediate vertices are drawn from the subset {1, 2, ..., k}. If we consider vertex k on the path then either:

·        k is not an intermediate vertex of p (i.e. is not used in the minimum weight path)

⇒ All intermediate vertices are in {1, 2, ..., k-1}

·        k is an intermediate vertex of p (i.e. is used in the minimum weight path)

⇒ We can divide p at k giving two subpaths p₁ and p₂ giving v_i ↝ k ↝ v_j

⇒ Subpaths p₁ and p₂ are shortest paths with intermediate vertices in {1, 2, ..., k-1}

Thus if we define a quantity d^(k)_ij as the minimum weight of the path from vertex i to vertex j with intermediate vertices drawn from the set {1, 2, ..., k} the above properties give the following recursive solution

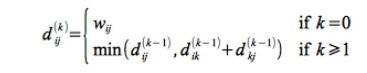
Thus we can represent the optimal values (when k = n) in a matrix as

Basically the algorithm works by repeatedly exploring paths between every pair using each vertex as an intermediate vertex. Since Floyd-Warshall is simply three (tight) nested loops, the run time is clearly O(V³).

Example:

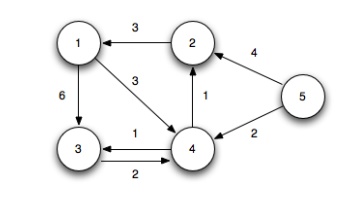
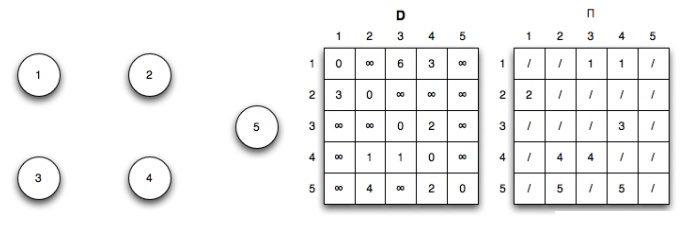
Initialization: (k = 0)

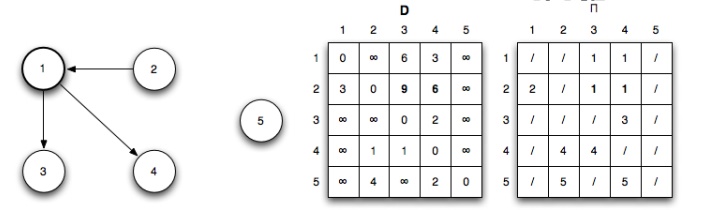
Iteration 1: (k = 1) Shorter paths from 2 ↝ 3 and 2 ↝ 4 are found through vertex 1

Iteration 2: (k = 2) Shorter paths from 4 ↝ 1, 5 ↝ 1, and 5 ↝ 3 are found through vertex 2

Iteration 3: (k = 3) No shorter paths are found through vertex 3

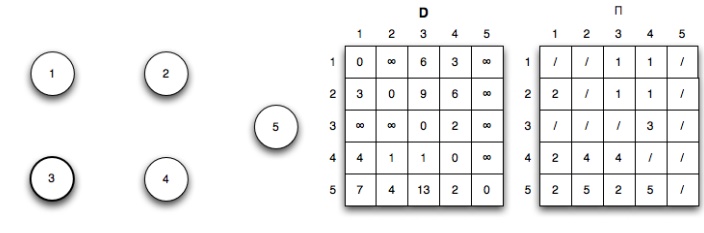
Iteration 4: (k = 4) Shorter paths from 1 ↝ 2, 1 ↝ 3, 2 ↝ 3, 3 ↝ 1, 3 ↝ 2, 5 ↝ 1, 5 ↝ 2, 5 ↝ 3, and 5 ↝ 4 are found through vertex 4

Iteration 5: (k = 5) No shorter paths are found through vertex 5

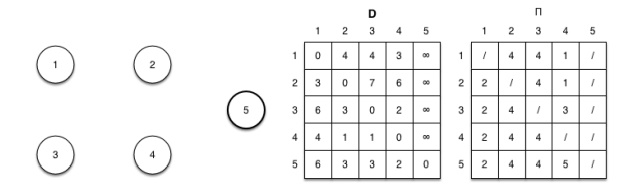
The final shortest paths for all pairs is given by

Transitive Closure

Floyd-Warshall can be used to determine whether or not a graph has transitive closure, i.e. whether or not there are paths between all vertices.

·        Assign all edges in the graph to have weight = 1

·        Run Floyd-Warshall

·     Check if all d_ij < n