Chapter: Programming and Data structures : Graphs
Kruskal's algorithm
KRUSKAL’S ALGORITHM
Kruskals
algorithm used for solving minimum spanning tree problem.
Procedure
i.
Initially there are |V| single node trees. Each
vertex is initially in its own set.
ii.
Select the edges (u,v) in the order of smallest
weight and accepted if it does not cause the cycle.
iii.
Adding an edge merges 2 trees into one.
iv.
Repeat step 2 until the tree contains all the
vertices.
The strategy
i.
The edges are built into a minheap structure and
each vertex is considered as a sigle node tree.
ii.
The deletemin operation is used to find the minimum
cost edge (u,v).
iii.
The vertices u and v are searched in the spanning
tree set S and if the returned sets are not same then (u,v) is added to the set
s with the constraint that adding (u,v) will not create a cycle in spanning
tree set S.
iv.
Repeat step (ii) and (iii) until a spanning tree is
constructed with |V| - 1 edges.
Example: Find the minimum spanning tree
for the following graph.
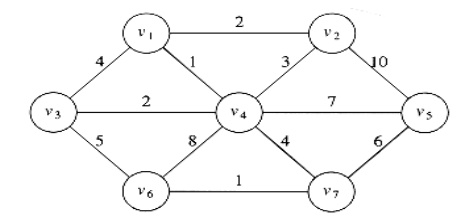
i.
Initially all the vertices are single node trees.
ii.
Select the smallest edge v1 to v4, both the nodes
are different sets, it does not form cycle.
iii.
Select the next smallest edge v6 to v7. These two
vertices are different sets; it does not form a cycle, so it is included in the
MST.
iv.
Select the next smallest edge v1 to v2. These two
vertices are different sets; it does not form a cycle, so it is included in the
MST.
v.
Select the next smallest edge v3 to v4. These two
vertices are different sets; it does not form a cycle, so it is included in the
MST.
vi.
Select the next smallest edge v2 to v4 both v2 and
v4 are same set, it forms cycle so v2 – v4 edge is rejected.
vii.
Select the next smallest edge v1 to v3, it forms
cycle so v1 – v3 edge is rejected.
viii.
Select the next smallest edge v4 to v7, it does not
form a cycle so it is included in the tree.
ix.
Select the next smallest edge v3 to v6, it forms a
cycle so v3 – v6 edge is rejected.
x.
Select the next smallest edge v5 to v7, it does not
form a cycle so it is included in the tree.

Figure: Action of Kruskal's algorithm on G
All the
nodes are included. The cost of minimum spanning tree = 16 (2 + 1+ 2 + 4 + 1 +
6).

Routine for kruskals algorithm
void
kruskal( graph G ) {
int EdgesAccepted; DisjSet S; PriorityQueue H;
vertex u, v; SetType uset, vset; Edge e;
Initialize( S ); //
form a single node tree
ReadGraphIntoHeapArray(
G, H );
BuildHeap(
H );
EdgesAccepted
= 0;
while(
EdgesAccepted < NumVertex-1 )
{
e = DeleteMin( H ); //
Selection of minimum edge
uset =
Find( u, S );
vset =
Find( v, S );
if( uset
!= vset )
{
/* accept
the edge */ EdgesAccepted++; SetUnion( S, uset, vset );
}
}
}
Related Topics