Dijkstra’s Algorithm

DIJKSTRA’S ALGORITHM:

Unweighted shortest Path

In unweighted shortest path, all the edges are assigned to 1.

Required Information

i.           known – Specifies whether the vertex is processed or not. It is set to 1 after it is processed, otherwise 0. Initially all vertices are unknown, so all entries marked as 0.

ii.           dv – it specifies distance form source to vertex. Initially all vertices are unreachable except for S whose path length is zero.

iii.           pv – It is book keeping variable, which allow us to print te actual path. i.e., the vertex which makes the changes in dv.

Procedure to find the unweighted shortest path

i.           Assign the source node as S and Enqueue S.

ii.           Dequeue the vertex S from queue and assign the value of that vertex to be known and then find its adjacency vertices.

iii.           If the distance of the adjacent vertices is equal to infinity then change the distance of that vertex as the distance of its source vertex. Increment by 1 and enqueue the vertex.

iv.          Repeat step ii until the queue becomes empty.

Routine for unweighted shortest path

void unweighted( Table T )

{

Queue Q; Vertex v, w;

Q = CreateQueue( NumVertex );

MakeEmpty( Q );

Enqueue( S, Q ); while( !IsEmpty( Q ) )

{

v = Dequeue( Q );

T[v].known = True;

for each w adjacent to v

if( T[w].Dist = = INFINITY )

{

T[w].Dist = T[v].Dist + 1;

T[w].path = v;

Enqueue( w, Q );

}}

DisposeQueue( Q ); /* free the memory */

}

Example

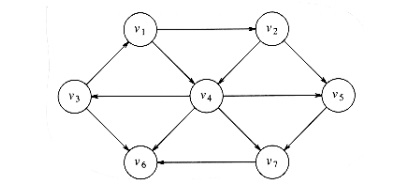
i.                   v3 is taken as source node and its path length is initialized to 0. v3 is inserted into Q.

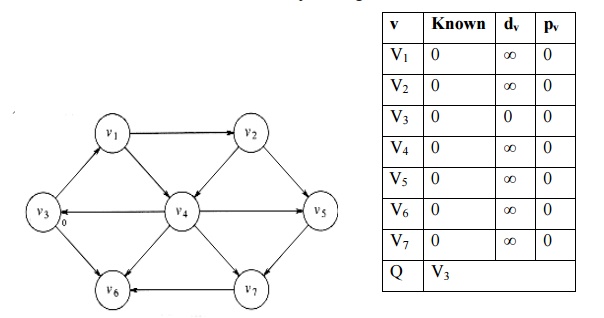
ii.           v3 find its adjacent node whose path length is 1. v1, v6 are adjacent nodes to v3 and inserted in to queue.

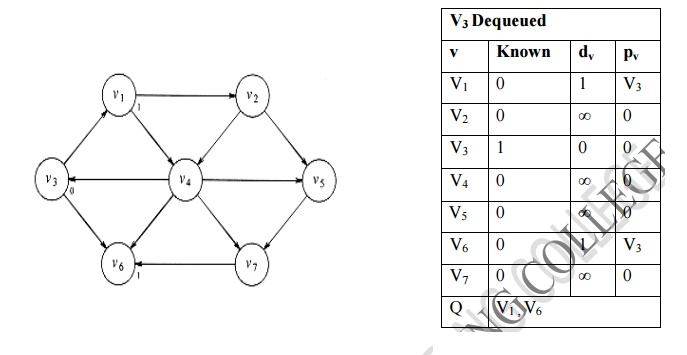
iii.           Find the adjacent node for v1. v2 and v4 are adjacent node for v1, v2 and v4 inserted into the queue.

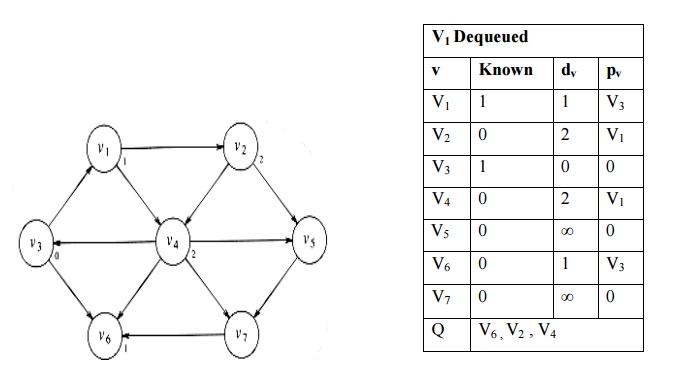
iv.          No adjacent vertices for v6. No change in path value for all vertices.

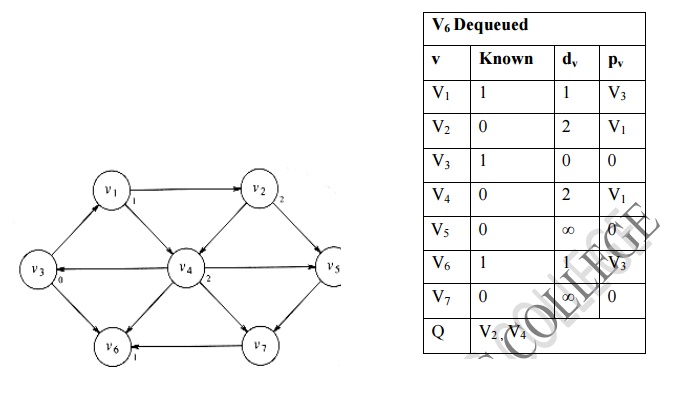
v.           Find the adjacent vertices for v2. v4 and v5 are adjacent nodes to v2 and inserted into queue.

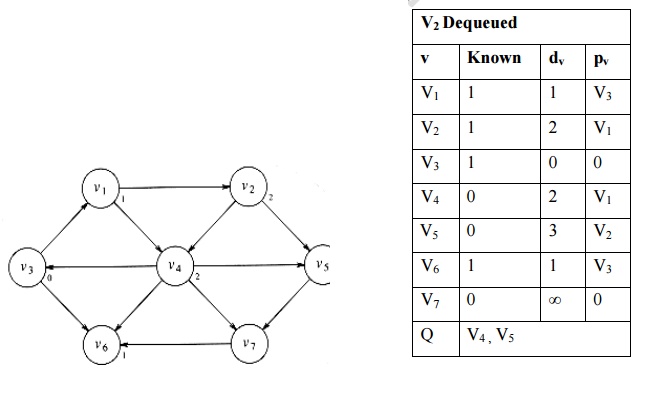
vi.          Find the adjacent vertices for v4. v5, v6 and v7 are adjacent vertices. Minimum path length for v7 is 3. v7 is inserted into queue.

vii.          An adjacent vertex for v5 is v7. Already found the minimum path length from v3 to v7 is 3. So no change in dv and pv.

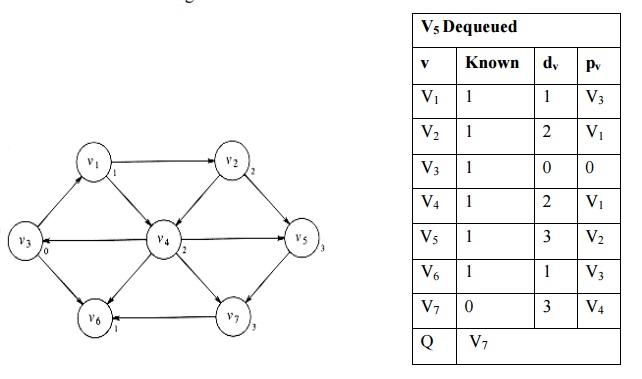
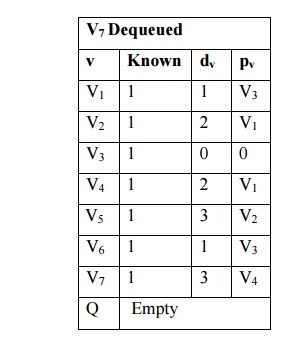
viii.          An adjacent vertex for v7 is v6. Already found the minimum path length from v3 to v6 is 1. So no change in dv and pv.

Algorithm Analysis

Running time is O(|E| + |V|)

Weighted Graph

The general method to solve the single source shortest path problem is known as

Dijkstra‟s algorithm. It applied to weighted graph.

Procedure

^Ø   It uses greedy technique.

^Ø   It proceeds in stages.

^Ø   It selects a vertex v, which has the smallest d_v among all the unknown vertices and declares the shortest path from s to v is known.

^Ø   The remainder consists of updating the value of d_w.

^Ø   We should  d_w = d_v + C_{v, w}, if the new value for d_w would an improvement.

Example: Find the shortest path for the following graph.

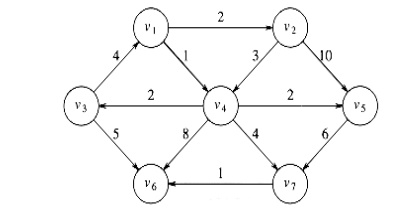
1.       v₁ is taken as source.

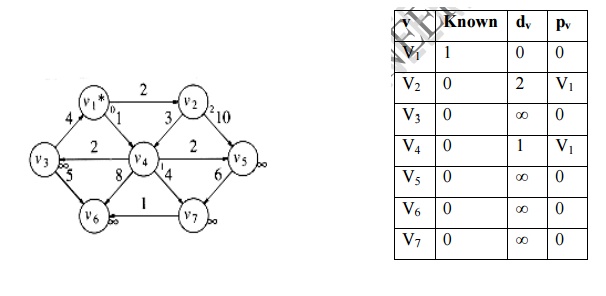
2.     Now v1 is known vertex, marked as 1. Its adjacent vertices are v₂, v₄, p_v and d_v values are updated

T[v₂]. dist = Min (T[v₂].dist, T[v₁].dist + Cv₁, v₂) = Min (α , 0+2) = 2 

T[v₄]. dist = Min (T[v₄].dist, T[v₁].dist + Cv₁, v₄) = Min (α , 0+1) = 1

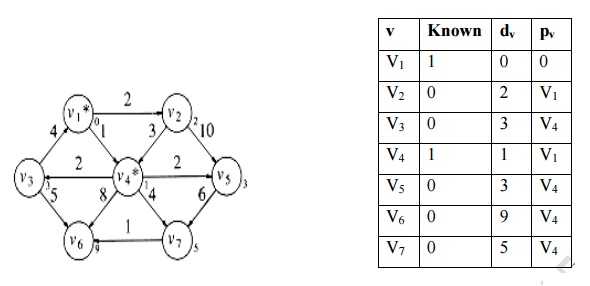
3.  Select the vertex with minimum distance away v₂ and v₄ . v₄ is marked as known vertex. Its adjacent vertices are v₃, v₅, v₆ and v₇ .

T[v₃]. dist = Min (T[v₃].dist, T[v₄].dist + Cv₄, v₃) = Min (α , 1+2) = 3

T[v₅]. dist = Min (T[v₅].dist, T[v₄].dist + Cv₄, v₅) = Min (α , 1+2) = 3

T[v₆]. dist = Min (T[v₆].dist, T[v₄].dist + Cv₄, v₆) = Min (α , 1+8) = 9

T[v₇]. dist = Min (T[v₇].dist, T[v₄].dist + Cv₄, v₇) = Min (α , 1+4) = 5

4.     Select the vertex which is shortest distance from source v₁. v₂ is smallest one. v₂ is marked as known vertex. Its adjacent vertices are v₄ ad v₅. The distance from v₁ to v₄ and v₅ through v₂ is more comparing with previous value of d_v. No change in d_v and p_v value.

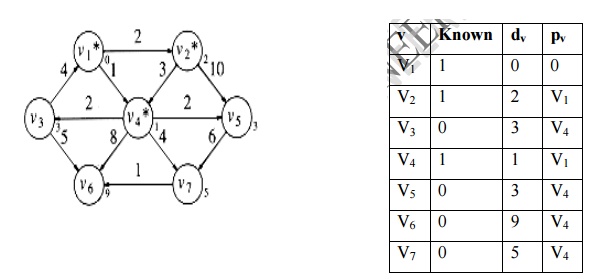
5.     Select tht smallest vertex from source. v₃ and v₅ are smallest one. Adjacent vertices for v₃ is v₁ and v₆. v₁ is source there is no change in dv and pv

T[v₆]. dist = Min (T[v₆].dist, T[v₃].dist + Cv₃, v₆) = Min (9 , 3+5) = 8

d_v and p_v values are updated. Adjacent vertices for v₅ is v₇. No change in d_v and p_v value.

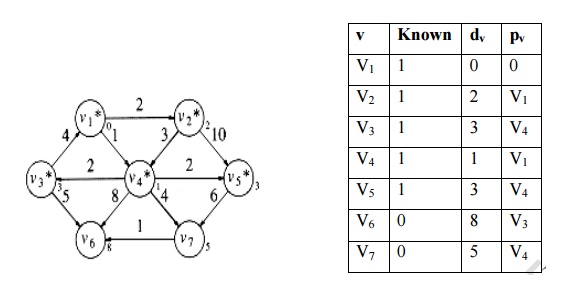
6. Next smallest vertex v₇. Its adjacent vertex is v₆. T[v₆]. dist = Min (T[v₆].dist, T[v₇].dist + Cv₇, v₆) = Min (8 , 5+1) = 6

d_v and p_v values are updated.

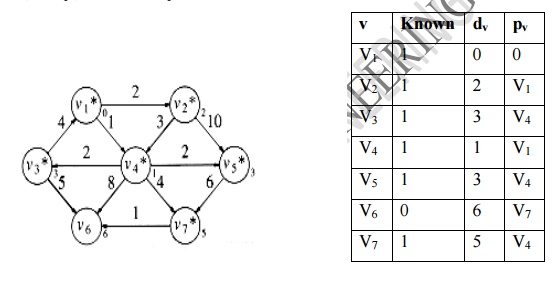
7. The last vertex v₆ is declared as known. No adjacent vertices for v₆. No updation in the table.

The shortest distance from source v₁ to all vertices. v₁ -> v₂ = 2

v₁ -> v₃ = 3 v₁ -> v₄ = 1 v₁ -> v₅ = 3 v₁ -> v₆ = 6 v₁ -> v₇ = 5

Algorithm Analysis

Time complexity of this algorithm

O(|E| + |V|² ) = O(|V|² )

Declarations for Dijkstra’s algorithm

typedef int Vertex; struct TableEntry

{

List header;          /* Adjacency List*/

int known;

DistType Dist;

Vertex Path

};

/* Vertices are numbered from 0*/ #define NotAVertex (-1)

typedef struct TableEntry Table[NumVertex];

Table Initialization routine

void InitTable(Vertex Start, Graph G, Table T)

{

int i; ReadGraph(G,T);

for (i=0; i<NumVertex; i++)

{

T[i].known = False;

T[i]. Dist = Infinity;

T[i]. Path = NotAVertex;

}

T[Start]. Dist = 0;

}

Routine to print the actual shortest path

void Printpath(Vertex V, Table T)

{

if(T[V]. Path != NotAVertex)

{

PrintPath(T[V]. Path, T); printf(“to”);

}

printf(“%v”, V);

/* %v is pseudocode*/

}

Pseudocode for Dijkstra’s algorithm

void Dijkstra(Table T)

{

Vertex v, w; for( ; ;)

{

v = smallest unknown distance vertex;

if( v = = NotAVertex)

break;

T[v]. kown = True;

for each w adjacent to v if(!T[w].known)

if(T[v].Dist + C_vw < T[w]. Dist)

{

/* update w*/

Decrease(T[w]. Dist to T[v].Dist + C_vw);

T[w]. path = v;

}

}

}