Prim’s Algorithm

PRIM’S ALGORITHM

In this method, minimum spanning tree is constructed in successive stages. One node is picked as a root and an edge is added (i.e) an associated vertex is added to the tree, until all the vertices are present in the tree with |V| - 1 edges.

The Strategy

i.            One node is picked as a root node (u) from the given connected graph.

ii.            At each stage choose a new vertex v from u, by considering an edge (u,v) with minimum cost among all edges from u, where u is already in the tree ad v is not in the tree.

iii.           The prims algorithm table is constructed with three parameters. They are

^Ø    known – known vertex i.e., processed vertex is indicated by 1. Unknown vertex is indicated by zero.

^Ø    d_v  - Weight of the shortest arc connecting v to the known vertex.

^Ø    p_v  - It contains last vertex (i.e.,) current vertex to cause a change in d_v.

iv.           After selecting the vertex v, the update rule is applied for each unknown w adjacent to v. The rule is d_w = min (d_w , C_w,v), that is more than one path exist between v to w then d_w is updated with minimum cost.

Example:

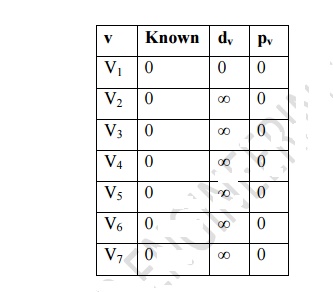
i.            v₁ is selected as initial node in the spanning tree and construct initial configuration of the table.

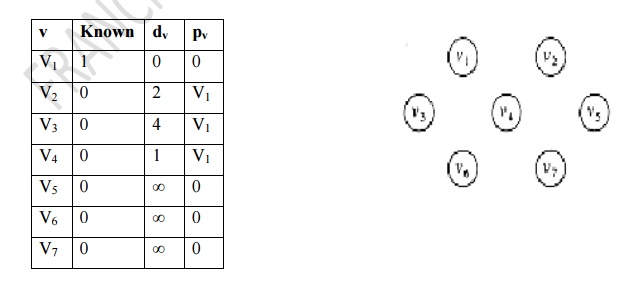
ii.           v1 is declared as known vertex. Then its adjacent vertices v2, v3, v4 are updated.

T[v₂].dist = min(T[v₂].dist, Cv₁,v₂) = min (∞ ,2) = 2

T[v₃].dist = min(T[v₃].dist, Cv₁,v₃) = min (∞ ,4) = 2

T[v₄].dist = min(T[v₄].dist, Cv₁,v₄) = min (∞ ,1) = 2

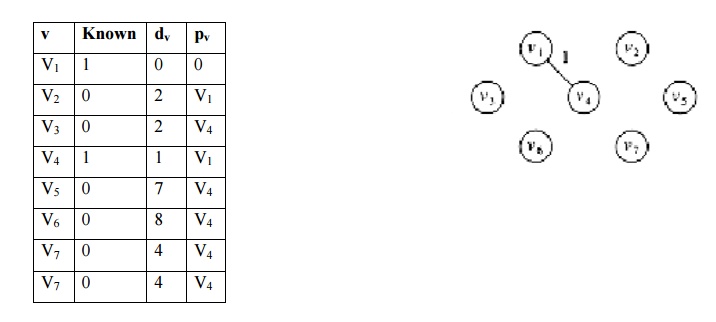
iii.           Among all adjacent vertices V_2, V_3, V_4. V₁ -> V₄ distance is small. So V₄ is selected and declared as known vertex. Its adjacent vertices distance are updated.

^ü   V₁  is not examined because it is known vertex.

^ü   No change in V₂ , because it has dv = 2 and the edge cost from V₄ -> V₂ = 3.

T[v₃].dist = min(T[v3].dist, Cv₄,v₃) = min (4 ,2) = 2

T[v₅].dist = min(T[v₅].dist, Cv₄,v₅) = min (∞ ,7) = 7

T[v₆].dist = min(T[v₆].dist, Cv₄,v₆ ) = min (∞ ,8) = 8

T[v₇].dist = min(T[v₇].dist, Cv₄,v₇ ) = min (∞ ,4) = 4

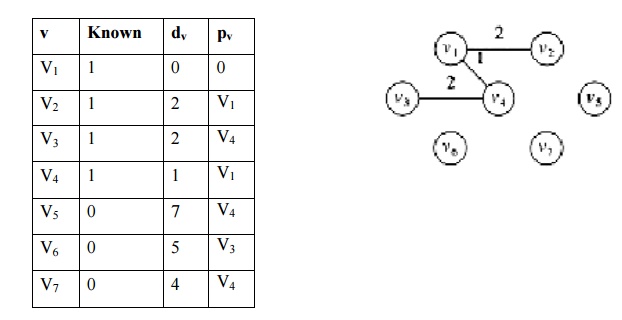
iv.          Among all either we can select v_2, or v₃ whose d_v  = 2, smallest among v_5, v₆ and v_7.

^ü   v₂ is declared as known vertex.

^ü   Its adjacent vertices are v1, v4 and v5. v1, v4 are known vertex, no change in their dv value.

T[v₅].dist = min(T[v5].dist, Cv₂,v₅) = min (7 ,10) = 7

v.           Among all vertices v3‟s dv value is lower so v3 is selected. v3‟s adjacent vertices are v1, v4 and v6. No changes in v1 and v4.

T[v₆].dist = min(T[v6].dist, Cv₃,v₆) = min (8 ,5) = 5

vi.      Among v5, v6, v7, v7‟s dv value is lesser, so v7 is selected. Its adjacent vertices are v4,

v4, and v6. No change in v4.

T[v5].dist = min(T[v5].dist, Cv7,v5) = min (7,6) = 6 T[v6].dist = min(T[v6].dist, Cv7,v6) = min (5,1) = 1

vii. Among v5 and v6, v6 is declared as known vertex. v6‟s adjacent vertices are v3, v4, and v7, no change in dv value, all are known vertices.

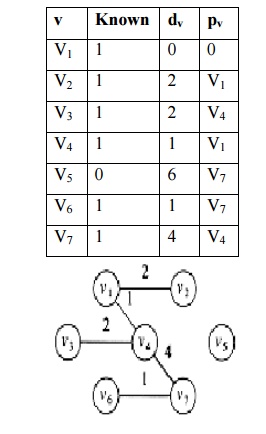
viii. Finally v5 is declared as known vertex. Its adjacent vertices are v2, v4, and v7, no change in dv value, all are known vertices.

The minimum cost of spanning tree is 16.

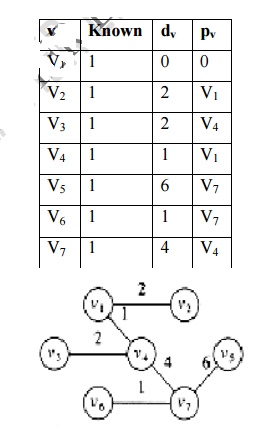
Algorithm Analysis

The runnig time is O(|V|²) in case of adjacency list and O(|E| log |V|) in case of binary

heap.

Prims Algorithm

i.            Consider any vertex in the graph.

ii.            Process the vertex and add the vertex to the tree.

iii.           Find the smallest edge from the graph connecting the edge of the vertex in the tree, such that it does not form a cycle.

iv.    Add the vertex to the tree.

v.    Repeat step 3 until the tree contains all the vertices in the graph.

Routine for prims Algorithm

void prims(Table T)

{

vertex v, w;

for( i=1; i<=Numvertex; i++)

{

T[i]. known = False;

T[i] . Dist = Infinity;

T[i]. path = 0;

}

for(;;)

{

//let v be the start vertex with the smallest distance T[v] . Dist = 0;

T[v]. known = true;

for each w adjacent to v if(!T[w] . known)

{

T[w] . Dist = Min(T[w]. Dist, C_v,w);

T[w]. path = v;

}

}

}