Topological Sort

TOPOLOGICAL SORT:

A topological sort is an ordering of vertices in a directed acyclic graph, such that if there is a path from v_i to v_j, then v_j appears after v_i in the linear ordering.

Topological ordering is not possible if the graph has a cycle, since for two vertices v and w on the cycle, v precedes w and w precedes v.

Steps for implementing the topological sort Step 1: Find the indegree for every vertex.

Step 2: Place te vertices whose indegree is 0 on the empty queue.

Step 3: Dequeue the vertex V and decrement the indegree‟s of all its adjacent vertices.

Step 4: Enqueue the vertex on the queue, if its degree falls to zero.

Step 5: Repeat from step 3 until the queue becomes empty.

Step 6: The topological ordering is the order in which the vertices dequeued.

Routine for Topological Sort

void Topsort( Graph G )

{

Queue Q;

int Counter = 0; Vertex V, W;

Q = CreateQueue( NumVertex );

MakeEmpty( Q );

for each vertex V

if( Indegree[V] = = 0 ) Enqueue( V, Q );

while( !IsEmpty( Q ) )

{

V = Dequeue( Q );

TopNum[V] = ++Counter; /* assign next number */ for each W adjacent to V

if( --Indegree[W] = 0 ) Enqueue( W, Q );

}

/                            if( Counter != NumVertex )

Error("Graph has a cycle");

DisposeQueue( Q ); /* free the memory */

}

Example: Find the topological sort for the following graph.

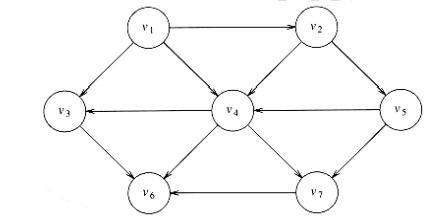
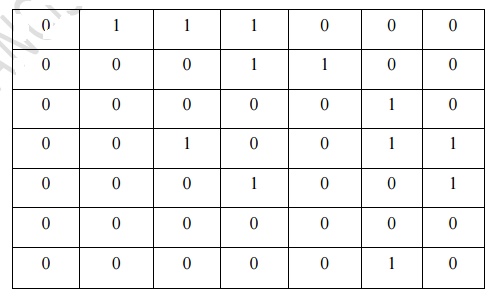
Adjacency Matrix

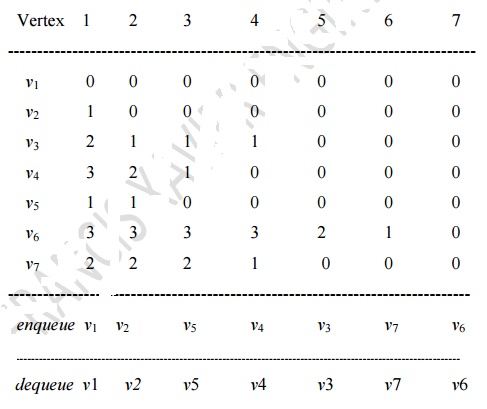
Solution

1.  Number of 1„s present in each column of adjacency matrix represents the indegree of

the corresponding vertex.

Indegree [V₁] = 0           Indegree [V₅] = 1

Indegree [V₂] = 1           Indegree [V₆] = 3

Indegree [V₃] = 2           Indegree [V₇] = 2

Indegree [V₄] = 3

2.     Enqueue the vertex, whose indegree is 0 and place it on the queue. Indegree of V₁ is 0. So place it in the queue.

3.     Dequeue the vertex V₁ from the queue and decrement the indegrees of its adjacent vertex V₂ & V_3. Indegree [V₂] = 0, Indegree [V₃] = 1. Now enqueue vertex V₂ because its indegree is 0.

4.     Dequeue the vertex V₂ from the queue and decrement the indegrees of its adjacent vertex V₂ & V_3. Indegree [V₂] = 0, Indegree [V₃] = 1. Now enqueue vertex V₂ because its indegree is 0.

Algorithm Analysis

The running time of this algorithm is O(|E| + |V|) where E represents the Edges and v represents the vertices of the graph.