Waves - Environmental factors affecting a floating construction in Sea Cages

Environmental factors affecting a floating construction

Waves

Waves are normally the limiting factor for site selection for cage aquaculture. If the wave height is too great it is very probable that this will affect the cage structure. Knowledge of the wave climate on the site will also be an important tool in choosing the correct cage technology and mooring system to avoid later breakages in cages and moorings. The trend towards using an increasing number of wave-exposed sites for marine cage farming is proving the importance of this.

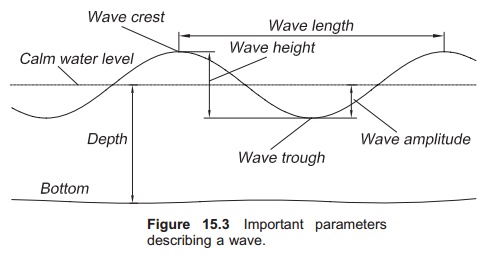
Several terms are used to describe a wave (Fig. 15.3):

·  Crest: the high point of the wave

·  Trough: the low point of the wave

·  Wave height: vertical distance between troughand crest – H (m)

·  Maximum wave height: highest measured waveheight – Hmax

·  Significant wave height: average wave height ofthe highest one-third of the waves recorded in a period. During a recording period there will always be a variation in the wave height. The significant wave height corresponds quite well with what an observer will record as the approximate wave height when looking at the waves over a period – Hs

·  Wave amplitude: distance from calm water levelto crest or trough; wave height divided by two (H/2) – a (m)

·  Wavelength: the horizontal distance between two following crests – L (m)

·  Wave period: the time taken for a wave crest to travel a distance equal to one wavelength – T (s)

·  Wave frequency: the inverse of the wave period; the same as the number of waves passing a given point per unit time – f (s−1).

Wave calculations

The description and calculation of waves and wave forces are quite difficult. Several textbooks are avail-able and may be consulted for further information (see, for example, refs 7–12). To illustrate what a wave is and how it moves, the water volume may be represented by many single water ‘particles’ which will be transported both vertically and horizontally with the wave (Fig. 15.4); they will move up with the crest and down with the trough. There is no net transport of water particles as long as the wave is not breaking (see below); they stay in the same place, but rotate in an orbit depending on the wave height and wave description. It is normally the current that causes the net transport of the water particles in the sea.

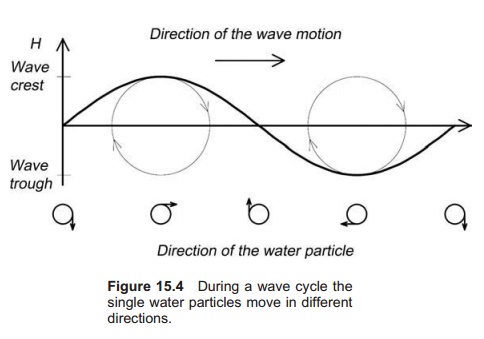
To understand how a wave is created the following simplified explanation can be used. Imagine that a stone is dropped into the water. As it displaces the water, the water particles are forced down and away. The energy that the stone adds to the water will be used to force neighbouring particles up. In this wave a wave is created. The wave continues to disperse until the wave motion is damped by friction between the water particles and no energy is left.

If an object such as a sea cage is lying in the water, the energy from the wave will also be transferred into this, and it will follow the wave motion. If an object is lying in the sea, however, the wave motions will be reduced because energy is used to move the object (see section 15.4.4).

To describe the wave motion, actually how a single water particle moves, several theories are used. The linear wave theory is the easiest and is also quite easy to understand, but several simplifications are made compared to real waves.11In most cases, however, this theory will suffice. The waves are described as sine waves, and all the standard geometrical knowledge of sine waves can be used to describe them. The single water particle rotates in a circular orbit where both the acceleration and velocity vary depending on where the particle is in the orbit: on top of the crest or down in the trough. However, under practical conditions the waves will not behave as sine waves. The wave is the sum of several wave systems coming from different directions, with different wave periods, height and phases (Fig. 15.5). This can be described by an irregular wave spectrum. Such spectra will vary from sea area to sea area. Spectra that are fitted to describe the wave for the different sea areas can be made based on actual measurements and calculations. For calculating wave motions according to developed wave spectra computer programs are used. In the linear wave theory, which is a simplification using sine waves, a set of formulae have been developed to calculate the wave motion and the total energy in the waves.

Depending on the depth, the wave will ‘travel’ in different ways. In shallow water the waves will have an effect all the way to the bottom; at intermediate depths the wave motion will be reduced closer to the bottom. In deep water the wave motion will quickly decrease; half a wavelength down there is almost no wave motion left because so much energy is used to move the surrounding sea. If the cages are located in the sea, deep-water conditions are commonly chosen. Here also is the explanation for the advantages of using submerged cages in water with high waves; at a depth of one wavelength there are no effects of the wave in deep water conditions.

Breaking, reflecting and diffraction of waves

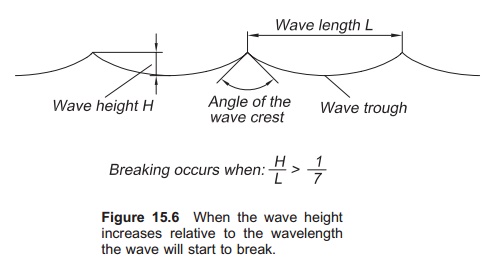
A wave ‘breaks’ when the height increases in relation to the wavelength (Fig. 15.6) and the wave gets steeper. White foam crests characterize a breaking wave visually. Much more energy is consumed when a wave starts to break. Under deep-water conditions wave breaking will occur under the following conditions:

H/L >1/7

where:

H =wave height

L =wavelength.

When a wave breaks there is net transport of water in the direction that the wave breaks.

Example

The wavelength is 30 m and the wave height is 5 m. Does the wave break?

H/L =5/30= 1/6 > 1/7

Therefore the wave will break.

If the wave height decreases to 3 m will the wave break now?

3/30 = 1/10 < 1/7

Therefore the wave does not break.

Reflection of a wave occurs when it hits an obstruction, such as the beach, a rock wall, a rock awash or a floating construction. If a vertical rock wall is hit by the wave an opposite wave motion is created and the energy in this wave will send the energy backwards. Under special conditions it can therefore be quite calm just outside such rocks, because the wave motions from the two different waves neutralize each other. If the wave hits the beach the depth will decrease and the wave will gradually start to break because it is forced up from the bottom and gets steeper. Breaking of waves can easily be seen when they hit the beach. Waves may not break before the beach, but when they hit the beach they start to break. The wave must get rid of all its stored energy when it reaches the land. How much is reflected is determined by the angle to the shore. Much energy is dispersed when the wave starts to break.

Diffraction occurs when a wave hits an obstruction; the angle at which the wave hits determines the direction of the diffracted wave. Diffraction may cause waves to be sent into areas that should be sheltered.

What creates waves?

Several factors may create waves but the most important are:

·                 Wind

·                 Human activity, such as shipping

·  Special natural phenomena such as earthquakes, land slips and underwater volcanic eruptions create waves known as tsunamis

·  Tide; waves with extremely long wavelengths are created.

Waves created by the wind are the most relevant to aquaculture facilities and are further described below. Shipping may also create waves that are unwanted on fish farms. To avoid such waves, sites close to heavily trafficked sea routes should be avoided. Waves created by exceptional natural phenomena (tsunamis) are difficult to avoid even if such phenomena occur more frequently in some areas than others. Tsunamis have a very long wave-length (>100 m) and a long period (around 1000 s). In such waves an enormous amount of energy is stored. They do not represent a great danger if a boat is on the sea, because the wavelength is so long. However, when they reach shallower water, and especially when they reach the shore and start to break, all the energy that is stored in them is released, and the consequences can be fatal. Such waves can be up to 30 m high when the shoreline has forced them to increase in height to dissipate their energy; they cause enormous destruction when they hit the shore. Waves created by the tide normally present no problems for cage farms. The wavelength here is so long that it is not interpreted as a wave, and the wave period is 12.5 h. Such waves can, however, create very strong tidal currents.

Wind created waves: The main ingredient in the formation of waves on the open ocean is wind. Wind created waves are normally also what inhibits site selection for cage farming. When winds blow across water, a drag is applied on the surface and pushes the water up, creating a wave. The height will increase as long as the wind is strong enough to add energy to the wave. After a period of time there will be equilibrium between the energy in the wind and the energy in the waves; the wave height will now be stable. Once a wave is generated, it will travel in the same direction until it meets land or is dampened by an opposing force such as winds blowing against it in the opposite direction, or by friction.

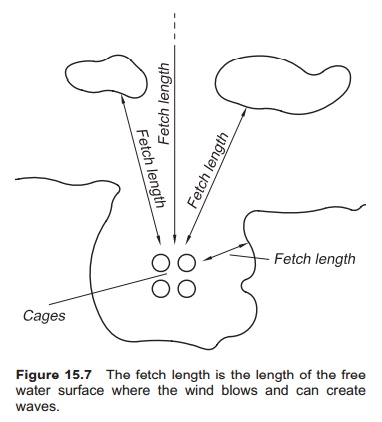
The height of wind created waves depends on the wind velocity (Uv), the duration of the wind (tv), the fetch length (F) and the presence of other waves when the wind begins to blow. The fetch length is the distance where wave development can take place (Fig. 15.7).

The Beaufort wind scale gives the expected wind velocity for the different wind strengths (see below). Some scales also present the normal wave height with different wind strengths; however, this is on open sea with no protection from land or islands.

In protected water the fetch length where the wind can blow will limit the ability of the wind to create waves. The fetch length can be read from a chart and is the length of the free water surface. If the fetch where the wind is blowing is narrow, as in a fjord, the wind effect will be less because of the friction against land on both sides reducing the velocity. To calculate the effective fetch length a compensation factor called the fetch length factor is used (Fig. 15.8). Calculations of effective fetch length in narrow fjords are given in the following two examples.

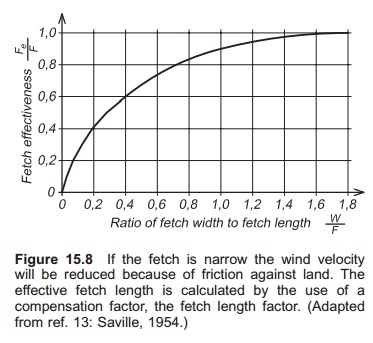
Example

The length where the wind blows is 10 km and the width of the fjord is 2 km.

Effective fetch length = fetch length × fetch length factor

In shallow water the Sverdrup–Munk–Bretsnei-der (SMB) method may be used to estimate wave height. Formulae and diagrams have been developed to find wave heights based on wind velocity (Uv), wind duration (tv) and effective fetch length (Fe) (Fig. 15.9). It must be remembered that some diagrams use the traditional sea units of foot (ft), knot (kn) and nautical mile (nm) (1 ft = 0.3048 m; 1 kn = 0.5144 m/s; 1 nm = 1852 m).

To use the diagram in Fig. 15.9, knowledge of the three factors, wind velocity (Uv), wind duration (tv) and effective fetch length (Fe) is required. First the wave height is found based on Uv and tv, and after-wards based on Uv and Fe. Of the two different values found, the lower will be the wave height on the site under the specified conditions because either wind duration or fetch length will limit the maximum wave height. For instance, if the wind duration is short a maximum wave height will not be attained; if the fetch length is also short it will also inhibit maximum development of waves, even if the wind duration indicates higher waves.

Example

Use SMB to estimate the wave height and wave period for a site if a fresh breeze of 20 kn blows for 2 h and the fetch length is 10 nm.

First calculate wind velocity and fetch length in SI units:

20 kn= 20 × 0.5144 m/s = 10.29 m/s

10 nm = 10 × 1.852 km = 18.5 km

Using wind velocity and duration criteria and Fig. 15.9

Significant wave height = ca. 0.6 m Significant wave period = ca. 3.3 s

Using wind velocity and fetch length criteria and Fig. 15.9

Significant wave height = ca. 0.8 m

Significant wave period = ca. 3.9 s

This means that wind duration is the limiting factor for development of waves; the wind does not blow long enough to create maximum wave height in pro-portion to the fetch length. Critical values for the site will therefore be:

Significant wave height = 0.6 m

Significant wave period = 3.3 s

The SMB method with the values and diagram given above may be used for depths greater than 15 m, which is normal in sea cage aquaculture. For intermediate depths and shallow water other for-mulae and diagrams apply.11

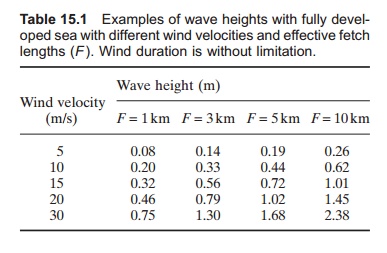
In open sea conditions with no limitation of the wind duration, the wave height will only depend on the effective fetch length and the wind velocity. The wave height created is the maximum possible with the given fetch length. A simplified method can then be used to calculate wave height in shallow water11 (Table 15.1):

Hs=5.112×10−4× UA F1/2(m)

Ts=6.238×10−2(UA F)1/3(s)

UA=0.71U1.23(m/s)

where:

U = wind velocity (10 min average value 10 mabove sea level) (m/s)

UA=adjusted wind velocity (m/s)

F = fetch length (m)

Hs = significant wave height (m)

ts = significant wave period (s).

The following may be used to estimate the maximum wave height from the significant wave height:

Hmax=1.9Hs

Example

Use the simplified method to calculate the significant wave height and wave period for a near gale with wind velocity of 15 m/s and fetch length of 3 km.

UA=0.71×27.96= 19.9 m/s

Hs=5.112×10−4×19.9×30001/2= 0.56 m

Ts=6.328×10−2×(19.9×3000)1/3= 2.44 s

Swell: Swell comprises wind generated wavescreated far away, which can also be called ocean waves; these may also affect cage farms when they come in from the sea. This is another reason for sitting cage farms in sheltered positions behind holms and breakwaters. Swells are characterized by quite large wave heights and long wavelengths. A swell can be recognized by its higher wave period compared to a local wind generated wave: typical swell periods are in the range 9–20 s, compared with 2–11 s for wind generated waves.