Water flow in channels and pipe systems

Water flow and head loss in channels and pipe systems

Water flow

The amount of water that flows through a pipe or in an open channel depends on the water velocity and the cross-sectional area of the pipe or the channel where the water is flowing. The following equation may be used for pipes and channels; it is also called the continuity equation:

Q = VA

where:

Q =water flow (l/min, l/s, m³/s) V =water velocity (m/s)

A =cross-sectional area of where the water is flow-ing. For full pipes the cross-sectional area will be the interior cross section of the pipe.

The above equation can be used as a basis for construction of a chart. If two of the sizes are known the last can be read from the chart and no calculation is necessary. Often the head loss is also included in the chart (see below).

Example

The water flow to a farm is 1000 l/min (0.0167 m³/s). The acceptable velocity in the pipeline is set at 1.5 m/s. Find the necessary pipe dimensions if one pipe is to be used.

                     = Q/V

                     = 0.0167/1.5 = 0.011 m²

Now

A =pr²

where:

r is the internal radius of the pipe and rearranging gives

The internal diameter in the pipe must therefore be 2 × 59 = 118 mm. Standard dimension pipes are available with an exterior diameter of 125 mm; a PN6 pipe with a wall thickness of 6 mm (supplier information) therefore has an internal diameter of 113 mm. This is actually slightly too small, but as the next stardard exterior dimension is 160 mm, it is best to choose the 125 mm pipe. This will result in the water velocity being slightly higher.

For an open channel the flow velocity depends on the slope, the hydraulic radius and the Manning coefficient. The Manning equation is used to calculate the flow velocity:

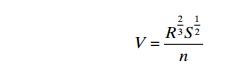
where:

V =average flow velocity in the channel R =hydraulic radius

S =channel slope

n =Manning coefficient.

The hydraulic radius is the ratio between the cross-sectional area where the water is flowing and the wetted perimeter, which is the length of the wetted surface of the channel measured normal to the flow.

R = cross-sectional area/ wetted perimeter

To achieve water transport through the channel it must be inclined. The slope is defined as the ratio between the difference in elevation between two points in the channel and the horizontal distance between the same two points.

Example

The horizontal distance between two points A and Bis 500 m. Point A is 34 m above sea level and point Bis 12 m above sea level. Calculate the slope (S) of the channel.

                     = (34 m − 12 m)/500 m

                  = 0.044

                  = 4.4 cm/m

This means that for each metre of elevation the horizontal distance is 22.7 m.

To ensure drainage, it is recommended that the slope is more than 0.0013, while self-cleaning is ensured with slopes in the range 0.005–0.010.

The Manning coefficient is determined by exper-iment, some actual values being about 0.015 for concrete-lined channels and 0.013 for plastic, while unlined channels made of straight and uniform earth have a value of 0.023 and those made of rock 0.025.

Based on the flow velocity and the cross-sectional area, the flow may rate be calculated with the con-tinuity equation which also can be expressed as:

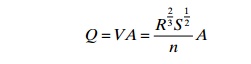
where:

Q =water flow

A =cross-sectional area where the water is flowing 

V =average flow velocity in the channel

R =hydraulic radius

S =slope of the channel 

n =Manning coefficient.