Vieta’s formula for Polynomial Equations

Vieta’s formula for Polynomial Equations

What we have learnt for quadratic polynomial, can be extended to polynomials of higher degree. In this section we study the relations of the zeros of a polynomial of higher degree with its coefficients. We also learn how to form polynomials of higher degree when some information about the zeros are known. In this chapter, we use either zeros of a polynomial of degree n or roots of polynomial equation of degree n .

(a) The Fundamental Theorem of Algebra

If  a  is  a  root  of  a  polynomial  equation P(x) = 0 ,  then  (x − a)  is  a  factor of P(x) . So, deg (P(x)) ≥ 1. If a and b are roots of P(x) = 0 then (x − a)(x − b) is a factor of P(x) and hence deg (P(x)) ≥ 2 . Similarly if P(x) = 0 has n roots, then its degree must be greater than or equal to n. In other words, a polynomial equation of degree n cannot have more than n roots.

In earlier classes we have learnt about “multiplicity”. Let us recall what we mean by “multiplicity”.

We know if (x − a)^k  is a factor of a polynomial equation P(x) = 0 and (x − a)^{k +1} is not a factor of the polynomial equation, P(x) = 0 , then a is called a root of multiplicity k . For instance, 3 is a root of multiplicity 2 for the equation x² − 6x + 9 = 0 and x³ − 7x² +159x − 9 = 0 . Though we are not going to use complex numbers as coefficients, it is worthwhile to mention that the imaginary number 2 + i is a root of multiplicity 2 for the polynomials x² − (4 + 2i)x + 3 + 4i = 0 and x⁴ − 8x³ + 26x² − 40x + 25 = 0.

If a is a root of multiplicity 1 for a polynomial equation, then a is called a simple root of the polynomial equation.

If P ( x) = 0 has n roots counted with multiplicity, then also, we see that its degree must be greater than or equal to n . In other words, “a polynomial equation of degree n cannot have more than n roots, even if the roots are counted with their multiplicities”.

One of the important theorems in the theory of equations is the fundamental theorem of algebra.

As the proof is beyond the scope of the Course, we state it without proof.

Theorem 3.1 (The Fundamental Theorem of Algebra)

Every polynomial equation of degree n ≥ 1 has at least one root in C.

Using this, we can prove that a polynomial equation of degree n has at least n roots in C when the   roots are counted with their multiplicities. This statement together with our discussion above says that

a polynomial equation of degree n has exactly n roots in C when the roots are counted with their multiplicities.

Some authors state this statement as the fundamental theorem of algebra.

(b) Vieta’s Formula

(i) Vieta’s Formula for Polynomial equation of degree 3

Now we obtain these types of relations to higher degree polynomials. Let us consider a general cubic equation

ax³ + bx² + cx + d = 0 .

By the fundamental theorem of algebra, it has three roots. Let α , β , and γ be the roots. Thus we have 

ax³ + bx² + cx + d = a(x − α )(x − β )(x − γ )

Expanding the right hand side, gives

ax³ − a(α + β + γ )x² + a(αβ + βγ + γα )x − a(αβγ ) .

Comparing the coefficients of like powers, we obtain

α + β + γ = −b/a , αβ + βγ + γα = c/a and αβγ = −d/a

Since the degree of the polynomial equation is 3, we have a ≠ 0 and hence division by a is meaningful. If a monic cubic polynomial has roots α , β , and γ , then

coefficient of x² = −(α + β + γ ) ,

coefficient of x = αβ + βγ + γα , and

constant term = −αβγ .

(ii) Vieta’s Formula for Polynomial equation of degree n > 3

The same is true for higher degree monic polynomial equations as well. If a monic polynomial equation of degree n has roots α₁ ,α₂ ,...,α_n , then

where Σα₁ denotes the sum of all roots, Σα₁α₂ denotes the sum of product of all roots taken two at a time,  Σα₁α₂α₃ denotes the sum of product of all roots taken three at a time, and so on. If  α , β ,γ , and δ are the roots of a quartic equation, then Σα₁ is written as Σα ,  Σα₁α₂   is written as  Σαβ and so on. Thus we have,

Σα = α + β + γ + δ

Σαβ = αβ + αγ + αδ + βγ + βδ + γδ

Σαβγ = αβγ + αβδ + αγδ + βγδ

Σαβγδ = αβγδ

When the roots are available in explicit numeric form, then also we use these convenient notations. We have to be careful when handling roots of higher multiplicity. For instance, if the roots of a cubic equation are 1, 2, 2, then ∑α = 5 and ∑αβ = (1× 2) + (1× 2) + (2 × 2) = 8 .

From the above discussion, we note that for a monic polynomial equation, the sum of the roots is the coefficient of xⁿ⁻¹ multiplied by (−1) and the product of the roots is the constant term multiplied by  (−1)ⁿ  .

Example 3.3

If α , β, and γ are the roots of the equation x³ + px² + qx + r = 0 , find the value of 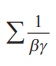  in terms of the coefficients.

Solution

Since α , β , and γ are the roots of the equation x³ + px² + qx + r = 0 , we have 

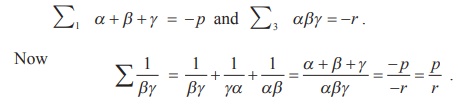
(c) Formation of Polynomial Equations with given Roots

We have constructed quadratic equations when the roots are known. Now we learn how to form polynomial equations of higher degree when roots are known. How do we find a polynomial equation of degree n with roots α₁ ,α₂, …. , α_n ? One way of writing a polynomial equation is multiplication of the factors. That is

( x − α₁ )( x − α₂ )( x − α₃ ) ...( x − αn ) = 0

is a polynomial equation with roots α₁ ,α₂ ,...,α_n. But it is not the usual way of writing a polynomial equation. We have to write the polynomial equation in the standard form which involves more computations. But by using the relations between roots and coefficients, we can write the polynomial equation directly; moreover, it is possible to write the coefficient of any particular power of x without finding the entire polynomial equation.

A cubic polynomial equation whose roots are α , β , and γ is

x³ − (α + β + γ ) x² + (αβ + βγ + γα ) x − αβγ = 0 .

A polynomial equation of degree n with roots α₁ ,α₂ ,K,α_n is given by

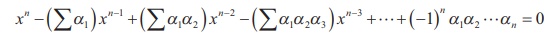
where,  ∑α₁ , ∑α₁α₂ , ∑α₁α₂α₃ ,K  are as defined earlier.

For instance, a polynomial equation with roots 1, −2 , and 3 is given by

x³ − (1− 2 + 3) x² + (1×(−2) + (−2)× 3 + 3×1) x −1×(−2)× 3 = 0

which, on simplification, becomes x³ − 2x² − 5x + 6 = 0 . It is interesting to verify that the expansion  of ( x −1)( x + 2)( x − 3) = 0 is x³ − 2x2 − 5x + 6 = 0 .

Example 3.4

Find the sum of the squares of the roots of ax⁴ + bx³ + cx² + dx + e  = 0 , a ≠ 0

Solution

Let   α , β ,γ ,  and  δ be the roots of ax⁴ + bx³ + cx² + dx + e = 0 .

Then, we get 

Example 3.5

Find the condition that the roots of cubic equation x³ + ax² + bx + c= 0 are in the ratio p : q : r .

Solution

Since roots are in the ratio p : q : r , we can assume the roots as pλ, qλ and rλ,

Then, we get 

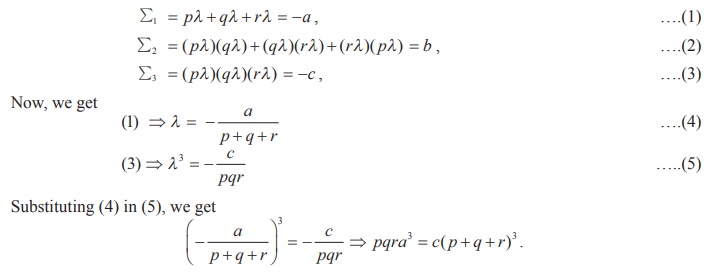
Example 3.6

Form the equation whose roots are the squares of the roots of the cubic equation

x³ + ax² + bx + c = 0 .

Solution

Let α , β , and γ be the roots of x³ + ax² + bx + c = 0 .

Then, we get 

Σ₁   = α + β + γ = -a , ….(1)

Σ₂  = αβ + βγ + γα = b , ….(2)

Σ₃   = αβγ = -c . ….(3)

We have to form the equation whose roots are α² , β² , and γ² .

Using (1), (2) and (3), we find the following:

Σ₁ = α² + β² + γ² = (α + β + γ )² - 2(αβ + βγ + γα ) = (-a)² - 2(b) = a² - 2b ,

Σ₂ = α² β²  + β²γ² + γ²α² = (αβ + βγ + γα )² - 2((αβ )(βγ ) + (βγ )(γα ) + (γα )(αβ ))

= (αβ + βγ + γα )² - 2αβγ (β + γ + α ) = (b)² - 2(-c)(-a) = b² - 2ca 

Σ₃ = α²β²γ² = (αβγ)² = (-c)² = c².

Hence, the required equation is

x³ – (α ² + β² + γ² ) x² + (α ² β ² + β²γ² + γ²α² ) x - α²β²γ² = 0.

That is,   x³  - (a²  - 2b) x²  + (b²  - 2ca) x - c²  = 0.

Example 3.7

If p is real, discuss the nature of the roots of the equation 4x² + 4 px + p + 2 = 0 , in terms of p 

Solution

The discriminant  Δ=(4 p)²  - 4 (4)( p + 2) = 16 ( p²  - p - 2) = 16 ( p +1)( p - 2) . So, we get 

Δ < 0 if -1 < p < 2

Δ = 0 if p = -1 or p = 2

Δ > 0 if -∞ < p < -1 or 2 < p < ∞

Thus the given polynomial has

imaginary roots if -1 < p < 2 ;

equal real roots if p = -1 or p = 2 ;

distinct real roots if -∞ < p < -1 or 2 < p < ∞ .