Non-polynomial Equations

Non-polynomial Equations

Some non-polynomial equations can be solved using polynomial equations. As an example let us consider the equation √(15-2x) = x. First we note that this is not a polynomial equation. Squaring both sides, we get x² + 2x −15 = 0 . We know how to solve this polynomial equation. From the solutions of the polynomial equation, we can analyse the given equation. Clearly 3 and −5 are solutions of x² + 2x −15 = 0 . If we adopt the notion of assigning only nonnegative values for √ •  then x = 3 is the only solution; if we do not adopt the notion, then we get x = −5 is also a solution.

Example 3.29

Find solution, if any, of the equation 2 cos2 x − 9 cos x + 4 = 0

Solution

The left hand side of this equation is not a polynomial in x . But it looks like a polynomial. In fact, we can say that this is a polynomial in cos x . However, we can solve equation (1) by using our knowledge on polynomial equations. If we replace cos x by y , then we get the polynomial equation 2y² - 9y + 4 = 0 for which 4 and 1/2 are solutions.

From this we conclude that x must satisfy cos x = 4 or cos x = 1/2. But cos x = 4 is never possible, if we take cos x = 1/2 , then we get infinitely many real numbers x satisfying cos x = 1/2 ; in fact, for all 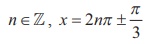  are solutions for the given equation (1).

If we repeat the steps by taking the equation cos²x - 9 cos x + 20 = 0, we observe that this equation has no solution.

Remarks

We note that

• not all solutions of the derived polynomial equation give a solution for the given equation;

• there may be infinitely many solutions for non-polynomial equations though they look like polynomial equations;

• there may be no solution for such equations.

• the Fundamental Theorem of Algebra is proved only for polynomials; for non-polynomial expressions, we cannot talk about degree and hence we should not have any confusion on the Fundamental Theorem of Algebra having non-polynomial equations in mind.