Exercise 3.6: Descartes Rule

EXERCISE 3.6

1. Discuss the maximum possible number of positive and negative roots of the polynomial equation 9x9 - 4x8 + 4x7 - 3x6 + 2x5 + x3 + 7x2 + 7x + 2 = 0.

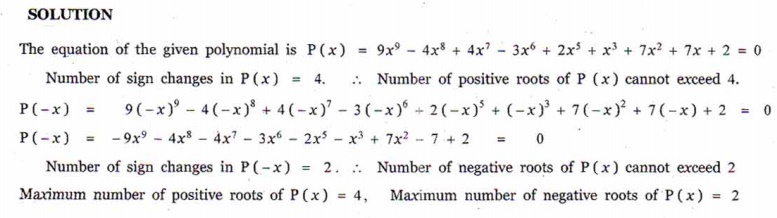
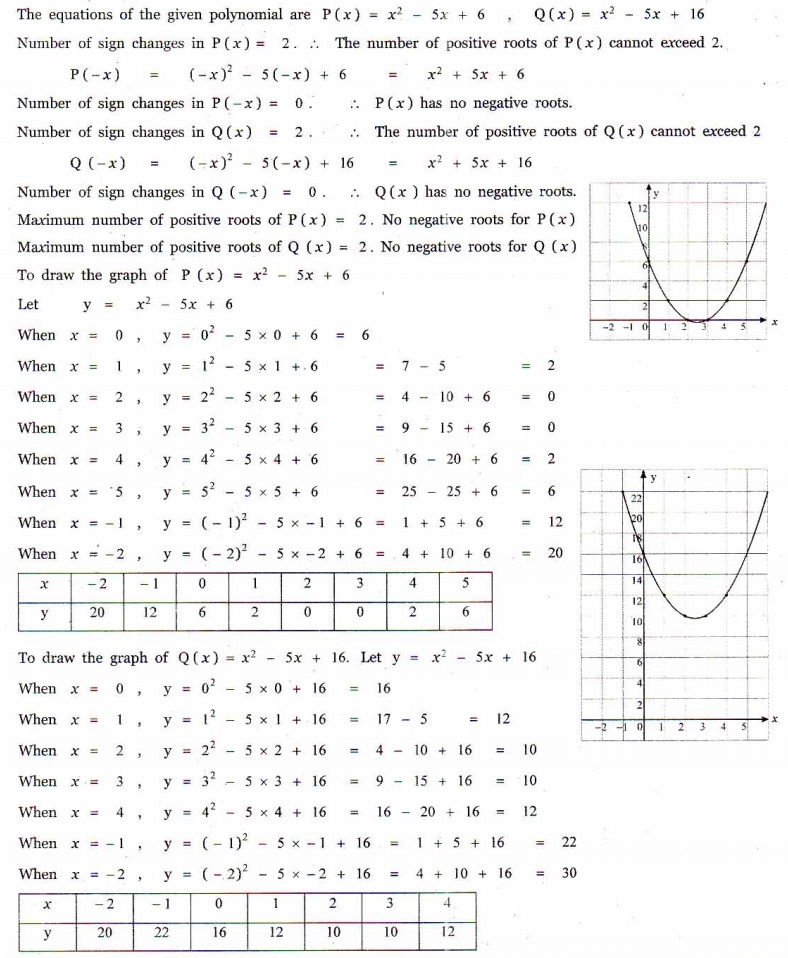
2. Discuss the maximum possible number of positive and negative zeros of the polynomials x2 - 5x + 6 and x2 - 5x +16 . Also draw rough sketch of the graphs.

3. Show that the equation x9 - 5x5 + 4x4 + 2x2 +1 = 0 has atleast 6 imaginary solutions.

4. Determine the number of positive and negative roots of the equation x9 - 5x8 -14x7 = 0 .

5. Find the exact number of real zeros and imaginary of the polynomial  x9 + 9x7 + 7x5 + 5x3 + 3x .

Answers:

1. It has at most four positive roots and at most two negative roots.

2. It has at most two positive roots and no negative roots.

4. It has one positive real root and one negative real root.

5. no positive real roots and no negative real roots.