Polynomials with Additional Information

Polynomials with Additional Information

Now we discuss a few additional information with which we can solve higher degree polynomials. Sometimes the additional information will directly be given, like, one root is 2 + 3i . Sometimes the additional information like, sum of the coefficients is zero, have to be found by observation of the polynomial.

1. Imaginary or Surds Roots

If  α + iβ  is an imaginary root of a quartic polynomial with real coefficients, then  α − iβ is  also a root; thus  (x − (α + iβ ))  and (x − (α − iβ )) are factors of the polynomial; hence their product is a factor; in other words, x² − 2αx + α² + β² is a factor; we can divide the polynomial with this factor and get the second degree quotient which can be solved by known techniques; using this we can find all the roots of the polynomial.

If 2+ √3 is a root of a quadric polynomial equation with rational coefficients, then 2 - √3 is also a root; thus their product (x-(2+√3)) (x-(2-√3)) is a factor; that is x² − 4x +1 is a factor; we can divide the polynomial with this factor and get the quotient as a second degree factor which can be solved by known techniques. Using this, we can find all the roots of the quadric equation. This technique is applicable for all surds taken in place of 2 + √3. 

If an imaginary root and a surd root of a sixth degree polynomial with rational coefficient are known, then step by step we may reduce the problem of solving the sixth degree polynomial equation into a problem of solving a quadratic equation.

Example 3.15

If 2 + i  and 3 - √2 are roots of the equation 

x⁶ -13x⁵ + 62x⁴ -126x³ + 65x² +127x -140 = 0 ,

find all roots.

Solution

Since the coefficient of the equations are all rational numbers, and 2 + i and 3 - √2 are roots, we get 2 - i and 3 + √2 are also roots of the given equation. Thus (x - (2 + i)), (x - (2 - i)), (x - (3 - √2)) and (x - (3 + √2)) are factors. Thus their product

((x - (2 + i))(x - (2 - i))(x - (3 - √2))(x - (3 + √2))

is a factor of the given polynomial equation. That is,

(x² - 4x + 5)(x² - 6x + 7)

is a factor. Dividing the given polynomial equation by this factor, we get the other factor as (x² - 3x - 4) which implies that 4 and -1 are the other two roots. Thus

2 + i, 2 - i, 3 + √2, 3 -√2, -1, and 4 

are the roots of the given polynomial equation.

2. Polynomial equations with Even Powers Only

If  P(x) is a polynomial equation of degree  2n , having only even powers of  x , (that is, coefficients of odd powers are 0 ) then by replacing  x²   by  y ,  we get a polynomial equation with degree  n  in  y;  let  y₁ , y₂  ,... y_n be the roots of this polynomial equation. Then considering the n equations x² = yr , we can find two values for x for each y_r ; these 2_n numbers are the roots of the given polynomial equation in x .

Example 3.16

Solve the equation x⁴ - 9x² + 20 = 0 .

Solution

The given equation is 

x⁴ - 9x² + 20 = 0 .

This is a fourth degree equation. If we replace x² by y , then we get the quadratic equation 

y2 - 9 y + 20 = 0 .

It is easy to see that 4 and 5 as solutions for y² - 9 y + 20 = 0 . Now taking x² = 4 and x² = 5 , we get  2, -2, √5, -√5 as solutions of the given equation.

We  note  that  the  technique  adopted  above  can  be  applied  to  polynomial  equations like x⁶ -17x³ + 30 = 0 , ax^2k + bx^k  + c = 0 and in general polynomial equations of the form a_n x^kn + a_n-1 x^{k (n-1)} +...+ a₁ x^k + a₀ = 0 where k is any positive integer.

3. Zero Sum of all Coefficients

Let P ( x) = 0 be a polynomial equation such that the sum of the coefficients is zero. What actually the sum of coefficients is? The sum of coefficients is nothing but P(1). The sum of all coefficients is zero means that P(1) = 0 which says that 1 is a root of P(x) . The rest of the problem of solving the equation is easy.

Example 3.17

Solve the equation x³ - 3x² - 33x + 35 = 0 .

Solution

The sum of the coefficients of the polynomial is 0. Hence 1 is a root of the polynomial. To find other roots, we divide x³ - 3x² - 33x + 35 by x -1 and get x² - 2x – 35 as the quotient. Solving this we get 7 and -5 as roots. Thus 1, 7, -5 form the solution set of the given equation.

4. Equal Sums of Coefficients of Odd and Even Powers

Let P ( x) = 0 be a polynomial equation such that the sum of the coefficients of the odd powers and that of the even powers are equal. What does actually this mean? If a is the coefficient of an odd degree in P ( x) = 0 , then the coefficient of the same odd degree in P (−x) = 0 is −a . The coefficients of even degree terms of both P(x) = 0 and P(−x) = 0 are same. Thus the given condition implies that the sum of all coefficients of P(−x) = 0 is zero and hence 1 is a root of P(−x) = 0 which says that −1 is a root of P(x) = 0 . The rest of the problem of solving the equation is easy.

Example 3.18

Solve the equation 2x³ +11x² - 9x -18 = 0.

Solution

We observe that the sum of the coefficients of the odd powers and that of the even powers are equal. Hence -1 is a root of the equation. To find other roots, we divide 2x³ +11x² - 9x -18 by x +1 and get 2x² + 9x -18 as the quotient. Solving this we get 3/2 and -6 as roots. Thus -6, -1, 3/2 are the roots or solutions of the given equation.

5. Roots in Progressions

As already noted to solve higher degree polynomial equations, we need some information about the solutions of the equation or about the polynomial. “The roots are in arithmetic progression” and “the roots are in geometric progression” are some of such information. Let us discuss an equation of this type.

Example 3.19

Obtain the condition that the roots of x³ + px² + qx + r = 0 are in A.P.

Solution

Let the roots be in A.P. Then, we can assume them in the form α - d ,α ,α + d .

Applying the Vieta’s formula (α - d ) + α + (α + d ) = - p/1 = p ⇒ 3α = - p ⇒ α =- p/3 .

But, we note that α is a root of the given equation. Therefore, we get

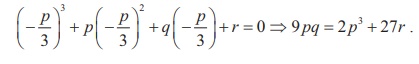
Example 3.20

Find the condition that the roots of ax³ + bx² + cx + d = 0 are in geometric progression. Assume a, b, c, d ≠ 0

Solution

Let the roots be in G.P.

Then, we can assume them in the form α/λ ,α ,α λ.

Applying the Vieta’s formula, we get

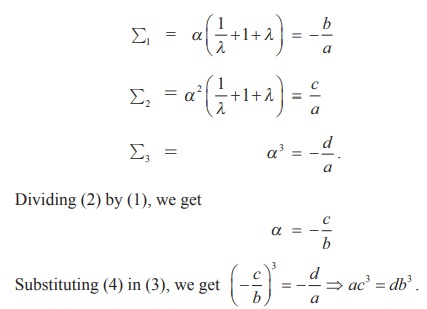
Example 3.21

If the roots of x³ + px² + qx + r = 0 are in H.P. , prove that 9 pqr = 27r³ + 2p.

Assume p, q, r ≠ 0

Solution

Let the roots be in H.P. Then, their reciprocals are in A.P. and roots of the equation 

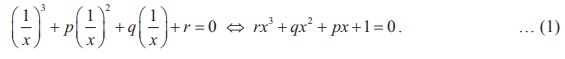
Since the roots of (1) are in A.P., we can assume them as α - d ,α ,α + d . 

Applying the Vieta’s formula, we get 

Σ₁ = (α - d ) + α + (α + d ) = - q/r ⇒ 3α = - q/r  ⇒ α =- q/3r .

But, we note that α is a root of (1). Therefore, we get

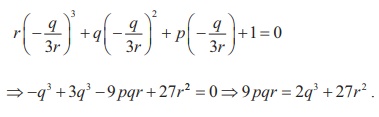
Example 3.22

It is known that the roots of the equation x³ - 6x² - 4x + 24 = 0 are in arithmetic progression. Find its roots.

Solution

Let the roots be a - d , a, a + d . Then the sum of the roots is 3a which is equal to 6 from the  given equation. Thus 3a = 6 and hence a = 2 . The product of the roots is a³ - ad² which is equal to -24 from the given equation. Substituting the value of a , we get 8 - 2d ² = -24 and hence d = ±4.

If we take d = 4 we get -2, 2, 6 as roots and if we take d = -4, we get 6, 2, -2  as roots (same roots given in reverse order) of the equation.