Irrational Roots

Irrational Roots

If we further restrict the coefficients of the quadratic equation ax2 + bx + c = 0 to be rational, we get some interesting results. Let us consider a quadratic equation ax2 + bx + c = 0 with a , b, and c rational. As usual let Δ = b2 − 4ac and let r1 and r2 be the roots. In this case, when Δ = 0 , we have r1 = r2 ; this root is not only real, it is in fact a rational number.

When Δ is positive, then no doubt that √Δ exists in R and we get two distinct real roots. But √Δ will be a rational number for certain values of a, b, and c , and it is an irrational number for other values of a, b , and c .

If √Δ is rational, then both r1 and r2 are rational.

If √Δ is irrational, then both r1 and r2 are irrational.

Immediately we have a question. If Δ > 0 , when will √Δ be rational and when will it be irrational? To answer this question, first we observe that Δ is rational, as the coefficients are rational numbers. So Δ = m/n for some positive integers m and n with (m, n) = 1 where (m, n) denotes the greatest common divisor of m and n. It is now easy to understand that √Δ is rational if and only if both m and n are perfect squares. Also, √Δ is irrational if and only if at least one of m and n is not a perfect square.

We are familiar with irrational numbers of the type p + √q where p and q are rational numbers and √q is irrational. Such numbers are called surds. As in the case of imaginary roots, we can prove that if p + √q  is a root of a polynomial, then p - √q  is also a root of the same polynomial equation, when all the coefficients are rational numbers. Though this is true for polynomial equation of any degree and can be proved using the technique used in the proof of imaginary roots, we state and prove this only for a quadratic equation in Theorem 3.3.

Before proving the theorem, we recall that if a and b are rational numbers and c is an irrational number such that a + bc is a rational number, then b must be 0 ; further if a + bc = 0 , then a and b must be 0.

For instance, if a + b√2 ∈ Q, then b must be 0 , and if a + b√2 = 0 then a = b = 0 . Now we state and prove a general result as given below.

Theorem 3.3

Let  p  and q be rational numbers such that √q  is irrational. If p + √q is a root of a quadratic equation with rational coefficients, then p − √q is also a root of the same equation.

Proof

We prove the theorem by assuming that the quadratic equation is a monic polynomial equation.

The result for non-monic polynomial equation can be proved in a similar way.

Let p and q be rational numbers such that √q is irrational. Let p + √q be a root of the equation x2 + bx + c = 0 where b and c are rational numbers.

Let α be the other root. Computing the sum of the roots, we get

α + p + √q = -b

and hence α + √q = -b - p ∈ Q. Taking -b - p as s , we have α + √q = s .

This implies that

α = s - √q.

Computing the product of the roots, gives

(s -√q )( p + √q) ) = c

and hence (sp - q) + (s - p) = c ∈ Q. Thus s - p = 0 . This implies that s = p and hence we get α = p – √q. So, the other root is p - √q.

Remark

The statement of Theorem 3.3 may seem to be a little bit complicated. We should not be in a hurry to make the theorem short by writing “for a polynomial equation with rational coefficients, irrational roots occur in pairs”. This is not true.

For instance, the equation x3 - 2 = 0 has only one irrational root, namely. 3√2. Of course, the other two roots are imaginary numbers (What are they?).

Example 3.9

Find a polynomial equation of minimum degree with rational coefficients, having 2 - √3 as a root.

Solution

Since 2 - √3 is a root and the coefficients are rational numbers, 2 + is also a root. A required polynomial equation is given by

       x2 - (Sum of the roots) x + Product of the roots = 0

and hence

x2 - 4x +1 = 0

is a required equation.

Note

We note that the term “rational coefficients” is very important; otherwise, x - (2 - √3) = 0 will be a polynomial equation which has 2 - √3 as a root but not 2 + √3. We state the following result without proof. 

Theorem 3.4

Let p and q be rational numbers so that √p and √q are irrational numbers; further let one  of √p and √q be not a rational multiple of the other. If √p + √q is a root of a polynomial equation with rational coefficients, then √p - √q , - √p + √q , and - √p - √q are also roots of the same polynomial equation.

Example 3.10

Form a polynomial equation with integer coefficients with   as a root.

Solution

Since  is a root, x –  is a factor. To remove the outermost square root, we take x +  as another factor and find their product

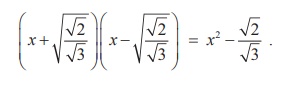
Still we didn’t achieve our goal. So we include another factor x2 + [√2/√3] and get the product 

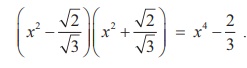
So, 3x4 - 2 = 0 is a required polynomial equation with the integer coefficients.

Now we identify the nature of roots of the given equation without solving the equation. The idea comes from the negativity, equality to 0, positivity of Δ = b2 - 4ac.