Partly Factored Polynomial

Partly Factored Polynomial

Quartic polynomial equations of the form (ax + b)(cx + d )( px + q)(rx + s)+ k = 0 , k ≠ 0 which can be rewritten in the form (αx²  + β x +λ) (αx²  + β x + µ)+ k = 0

We illustrate the method of solving this situation in the next two examples.

Example 3.23

Solve the equation 

(x - 2)(x - 7)(x - 3)(x + 2) +19 = 0.

Solution

We can solve this fourth degree equation by rewriting it suitably and adopting a technique of substitution. Rewriting the equation as

(x - 2)(x - 3)(x - 7)(x + 2) +19 = 0 . 

the given equation becomes 

(x² - 5x + 6)(x² - 5x -14) +19 = 0 .

If we take x² - 5x as y , then the equation becomes ( y + 6)( y -14) +19 = 0;

that is,

y² - 8 y – 65 = 0 .

Solving this we get solutions y = 13 and y = -5 . Substituting this we get two quadratic equations

x² - 5x -13 = 0 and x² - 5x + 5 = 0

which can be solved by usual techniques. The solutions obtained for these two equations together give solutions as

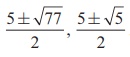
Example 3.24

Solve the equation (2x - 3)(6x -1)(3x - 2)(x -12) – 7 =  0 .

Solution

The given equation is same as 

(2x - 3)(3x - 2)(6x -1)(x -12) – 7 =  0 .

After a computation, the above equation becomes 

(6x² -13x + 6)(6x² -13x +12) – 7 =  0 .

By taking y = 6x² -13x, the above equation becomes, 

( y + 6)( y +12) - 7 = 0

which is same as

y² +18 y + 65 = 0 .

Solving this equation, we get y = -13 and y = -5 .

Substituting the values of y in y = 6x2 -13x, we get

6x² -13x + 5 =  0

6x² -13x +13 =  0

Solving these two equations, we get

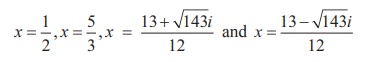
as the roots of the given equation.