Reciprocal Equations

Reciprocal Equations

Let α be a solution of the equation.

2x⁶ - 3x⁵ + √2x⁴ + 7x³ + √2x² - 3x + 2 = 0. ... (1)

Then α ¹ 0 (why?) and

2α⁶ - 3α⁵ + √2α⁴ + 7α³ + √2α² - 3α + 2 = 0.

 Substituting 1/α for x in the left side of (1), we get

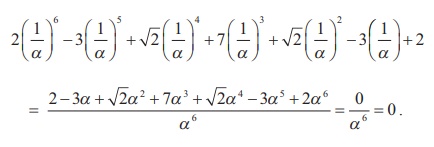
Thus 1/α is also a solution of (1). Similarly we can see that if α is a solution of the equation

 x⁵ + 3x⁴ - 4x³ + 4x² - 3x – 2 = 0 ... (2)

then 1/α is also a solution of (2).

Equations (1) and (2) have a common property that, if we replace x by 1/x in the equation and write it as a polynomial equation, then we get back the same equation. The immediate question that flares up in our mind is “Can we identify whether a given equation has this property or not just by seeing it?” Theorem 3.6 below answers this question.

Definition 3.1

A polynomial P(x) of degree n is said to be a reciprocal polynomial if one of the following conditions is true:

A polynomial P(x) of degree n is said to be a reciprocal polynomial of Type I if P(x) = 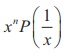 called a reciprocal equation of Type I.

A polynomial P(x) of degree n is said to be a reciprocal polynomial of Type II if P(x) = - 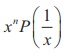 called a reciprocal equation of Type II.

Theorem 3.6

A polynomial equation a_n xⁿ + a_n−1 xⁿ⁻¹ + a_n−2 xⁿ⁻² +….+ a₂ x² + a₁ x + a₀ = 0 , (a_n≠ 0) is a reciprocal equation if, and only if, one of the following two statements is true:

(i) a_n = a₀ , a_n-1  = a₁ ,       a_n-2 = a₂ ….

(ii) a_n = - a₀ , a_n-1 = - a₁ , a_n-2 =  - a₂ , … 

Proof

Consider the polynomial equation

P(x) =  a_n xⁿ + a_n-1 x^n-1 + a_n-2 x^n-2 +...+ a₂ x² + a₁ x + a₀ = 0 .   … (1)

Replacing x by 1/x in (1), we get

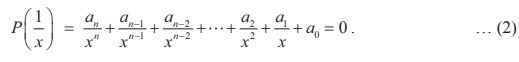
Multiplying both sides of (2) by xⁿ, we get

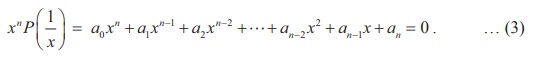
Now, (1) is a reciprocal equation  ⇔  P(x) = ± xⁿ P (1/x) ⇔ (1) and (3) are same .

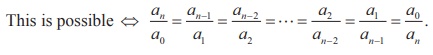
Let the proportion  be  equal to λ. Then, we get a_n/a₀ = λ  and a₀/a_n = λ . Multiplying these equations, we get λ² = 1. So, we get two cases λ = 1 and λ = -1 .

Case (i) :

λ = 1 In this case, we have a_n = a₀ , a_n−1 = a₁ , a_n−2 = a₂ , …..

That is, the coefficients of (1) from the beginning are equal to the coefficients from the end.

Case (ii) :

λ = −1 In this case, we have a_n = −a₀ , a_n−1 = −a₁ , a_n−2 = −a₂ , …..

That is, the coefficients of (1) from the beginning are equal in magnitude to the coefficients from the end, but opposite in sign.

Note

Reciprocal equations of Type I correspond to those in which the coefficients from the beginning are equal to the coefficients from the end.

For instance, the equation 6x⁵ + x⁴ − 43x³ − 43x² + x + 6 = 0 is of type I.

Reciprocal equations of Type II correspond to those in which the coefficients from the beginning are equal in magnitude to the coefficients from the end, but opposite in sign.

For instance, the equation 6x⁵ − 41x⁴ + 97x³ − 97x2 + 41x − 6 = 0 is of Type II.

Remark

(i) A reciprocal equation cannot have 0 as a solution.

(ii) The coefficients and the solutions are not restricted to be real. 

(iii) The statement “If P(x) = 0 is a polynomial equation such that whenever α is a root, 1/α is also a root, then the polynomial equation P ( x) = 0 must be a reciprocal equation” is not true. For instance 2x³ − 9x² + 12x − 4 = 0 is a polynomial equation whose roots are 2, 2,1/2.

Note that x³ P( 1/x) ≠ ± P(x) and hence it is not a reciprocal equation. Reciprocal equations are classified as Type I and Type II according to a_n-r = a_r or a_n-r = -a_r , r = 0, 1, 2,...n. We state some results without proof :

·               For an odd degree reciprocal equation of Type I, x = −1 must be a solution.

·               For an odd degree reciprocal equation of Type II, x = 1 must be a solution.

·               For an even degree reciprocal equation of Type II, the middle term must be 0 Further x = 1 and x = −1 are solutions.

• For an even degree reciprocal equation, by taking x + (1/x) or x – (1/x) as y , we can obtain a polynomial equation of degree one half of the degree of the given equation ; solving this polynomial equation, we can get the roots of the given polynomial equation.

As an illustration, let us consider the polynomial equation

6x⁶ - 35x⁵ + 56x⁴ - 56x² + 35x - 6 = 0

which is an even degree reciprocal equation of Type II. So 1 and -1 are two solutions of the equation and hence x² -1 is a factor of the polynomial. Dividing the polynomial by the factor x² -1, we get 6x⁴ - 35x³ + 62x² - 35x + 6 as a factor. Dividing this factor by x2 and rearranging the terms we get . Setting u = ( x + 1/x)  it becomes a quadratic polynomial as 6 (u² - 2) - 35u + 62 which reduces to 6u² - 35u + 50 . Solving we obtain u = 10/3 , 5/2 . Taking u = 10/3 gives x = 3, 1/3 and taking u = 5/2 gives x = 2, 1/2. So the required solutions are +1, -1, 2, 1/2 , 3, 1/3 .

Example 3.27

Solve the equation 7x³ − 43x² = 43x − 7.

Solution

The given equation can be written as 7x³ - 43x² - 43x + 7 = 0.

This is an odd degree reciprocal equation of Type I. Thus -1 is a solution and hence x +1 is a factor.

Dividing the polynomial 7x³ - 43x² - 43x + 7 by the factor x +1,we get 7x² - 50x + 7 as a quotient.

Solving this we get 7 and 1/7 as roots. Thus -1, 1/7 , 7 are the solutions of the given equation.

Example 3.28

Solve the following equation: x⁴ −10x³ + 26x² −10x +1 = 0.

Solution

This equation is Type I even degree reciprocal equation. Hence it can be rewritten as 

Let y = x + [1/x] . Then, we get

(y²  - 2) -10 y + 26 = 0 ⇒ y² -10 y + 24 =  0   ⇒  ( y -6)( y - 4) = 0 ⇒   y = 6  or  y = 4

Case (i)

y = 6 ⇒   x + (1/x) = 6  ⇒ x = 3 + 2√2, x = 3 -√2 .

Case (ii)

y = 4 ⇒  x + (1/x) = 4  ⇒  x = 2 + √3, x = 2 -√3

Hence, the roots are 3  ± 2√2, 2 ±√3