Imaginary Roots

Imaginary Roots

For a quadratic equation with real coefficients, if α + iβ is a root, then α − iβ is also a root. In this section we shall prove that this is true for higher degree polynomials as well.

We now prove one of the very important theorems in the theory of equations.

Theorem 3.2 (Complex Conjugate Root Theorem)

If a complex number z0  is a root of a polynomial equation with real coefficients, then its complex conjugate 0 is also a root.

Proof

Let P ( x) = an xn + an-1 xn-1 +...+ a1 x + ao = be a polynomial equation with real coefficients.

Let z0 be a root of this polynomial equation. So, P( z0) = 0. Now

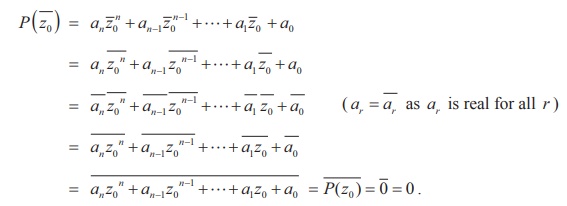
That is P(0 ) = 0 ; this implies that whenever z0 is a root (i.e. P( z0 )=0), its conjugate 0  is also a root.

If one asks whether 2 is a complex number, many students hesitate to say “yes”. As every integer is a rational number, we know that every real number is also a complex number. So to clearly specify a complex number that is not a real number, that is to specify numbers of form α + iβ  with  β ± 0 , we use the term “non-real complex number”. Some authors call such a number an imaginary number.

Remark 1

Let z0  = α + iβ with β ± 0 . Then 0   = α - iβ . If α + iβ is a root of a polynomial equation P(x) = 0 with real coefficients, then by Complex Conjugate Root Theorem,  α - iβ   is also a root of P(x) = 0 .

Usually the above statement will be stated as complex roots occur in pairs; but actually it means that non-real complex roots or imaginary roots occur as conjugate pairs, being the coefficients of the polynomial equation are real.

Remark 2

From this we see that any odd degree polynomial equation with real coefficients has at least one real root; in fact, the number of real roots of an odd degree polynomial equation with real coefficients is always an odd number. Similarly the number of real roots of an even degree polynomial equation with real coefficients is always an even number.

Example 3.8

Find the monic polynomial equation of minimum degree with real coefficients having 2 - √3 i as a root.

Solution

Since 2 - √3i is a root of the required polynomial equation with real coefficients, 2 + √3i is also a root. Hence the sum of the roots is 4 and the product of the roots is 7 . Thus x2 - 4x + 7 = 0 is the required monic polynomial equation.