Basics and types of Polynomial Equations

Basics of Polynomial Equations

1. Different types of Polynomial Equations

We already know that, for any non–negative integer n , a polynomial of degree n in one variable

x is an expression given by

P ≡ P(x)= a_n xn + a_n-1 xn-1 +...+ a₁ x + a₀             ……….(1)

where a_r ∈ C are constants, r = 0,1, 2,K, n with a_n ≠ 0 . The variable x is real or complex.

When all the coefficients of a polynomial P are real, we say “P is a polynomial over R ”. Similarly we use terminologies like “P is a polynomial over C ”, “P is a polynomial over Q”, and P is a polynomial over Z ”

The function P defined by P ( x) = a_n xⁿ + a_n−1 xⁿ⁻¹ +...+ a₁x + a₀ is called a polynomial function. 

The equation

an xn + a_n-1 x^n-1 +...+ a₁ x + a₀ = 0              ……….(2)

is called a polynomial equation.

If a_ncⁿ + a_n−1cⁿ⁻¹ +...+ a₁c + a₀ = 0 for some c ∈ C , then c is called a zero of the polynomial (1) and root or solution of the polynomial equation (2).

If c is a root of an equation in one variable x, we write it as“ x = c is a root”. The constants a_r are called coefficients. The coefficient a_n is called the leading coefficient and the term a_nxⁿ is called the leading term. The coefficients may be any number, real or complex. The only restriction we made is that the leading coefficient a_n is nonzero. A polynomial with the leading coefficient 1 is called a monic polynomial.

Remark:

We note the following:

·               Polynomial functions are defined for all values of x .

·               Every nonzero constant is a polynomial of degree 0 .

·               The constant 0 is also a polynomial called the zero polynomial; its degree is not defined.

·               The degree of a polynomial is a nonnegative integer.

·               The zero polynomial is the only polynomial with leading coefficient 0 .

·               Polynomials of degree two are called quadratic polynomials.

·               Polynomials of degree three are called cubic polynomials.

·               Polynomial of degree four are called quartic polynomials.

It is customary to write polynomials in descending powers of x . That is, we write polynomials having the term of highest power (leading term) as the first term and the constant term as the last term.

For instance, 2x +3y +4z= 5 and 6x² + 7x² y³ + 8z =9 are equations in three variables x , y , z ; x²- 4x + 5 =0 is an equation in one variable x. In the earlier classes we have solved trigonometric equations, system of linear equations, and some polynomial equations.

We know that 3 is a zero of the polynomial x² − 5x + 6 and 3 is a root or solution of the equation x² − 5x + 6 = 0 . We note that cos x = sin x and cos x + sin x = 1 are also equations in one variable x.

However, cos x − sin x and cos x + sin x −1 are not polynomials and hence cos x = sin x and cos x + sin x = 1 are not “polynomial equations”. We are going to consider only “polynomial equations” and equations which can be solved using polynomial equations in one variable.

We recall that sin² x + cos² x = 1 is an identity on R , while sin x + cos x = 1 and sin² x + cos² x = 1 are equations.

It is important to note that the coefficients of a polynomial can be real or complex numbers, but the exponents must be nonnegative integers. For instance, the expressions 3x⁻² +1 and 5x^1/2 +1 are not polynomials. We already learnt about polynomials and polynomial equations, particularly about quadratic equations. In this section let us quickly recall them and see some more concepts.

2. Quadratic Equations

For the quadratic equation ax² + bx + c =0, b² - 4ac is called the discriminant and it is usually denoted by Δ. We know that 

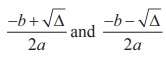
are roots of the ax² + bx + c = 0 . The two roots together are usually written as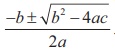 

It is unnecessary to emphasize that a ≠ 0 , since by saying that ax² + bx + c is a quadratic polynomial, it is implied that a ≠ 0.

• ∆ > 0 if, and only if, the roots are real and distinct

• ∆ < 0 if, and only if, the quadratic equation has no real roots.