Definition, Theorem, Formulas, Solved Example Problems | Theory of Equations - Vieta’s formula for Polynomial Equations | 12th Mathematics : UNIT 3 : Theory of Equations
Chapter: 12th Mathematics : UNIT 3 : Theory of Equations
Vieta’s formula for Polynomial Equations
Vieta’s formula for Polynomial Equations
What we have learnt for quadratic polynomial, can be extended to
polynomials of higher degree. In this section we study the relations of the
zeros of a polynomial of higher degree with its coefficients. We also learn how
to form polynomials of higher degree when some information about the zeros are
known. In this chapter, we use either zeros of a polynomial of degree n or
roots of polynomial equation of degree n .
(a) The Fundamental Theorem of Algebra
If a is a root of
a polynomial equation P(x)
= 0 , then
(x − a)
is a factor of P(x) . So, deg (P(x)) ≥ 1. If a and b
are roots of P(x) = 0 then (x − a)(x − b) is a factor of P(x) and hence deg (P(x)) ≥ 2 . Similarly if P(x)
= 0 has n roots,
then its degree must be greater than or equal to n. In other words, a polynomial equation of
degree n cannot have more than n roots.
In earlier classes we have learnt about “multiplicity”. Let us
recall what we mean by “multiplicity”.
We know if (x − a)k is a factor of a polynomial equation P(x)
= 0 and (x − a)k +1 is not a factor of
the polynomial equation, P(x)
= 0 , then a is
called a root of multiplicity k . For instance, 3 is a root of multiplicity 2
for the equation x2 − 6x + 9 = 0 and x3 − 7x2 +159x − 9 = 0 . Though we are not going to use complex numbers as
coefficients, it is worthwhile to mention that the imaginary number 2 + i is a root of
multiplicity 2 for the polynomials x2 − (4 + 2i)x + 3 + 4i = 0 and x4 − 8x3 + 26x2 − 40x + 25 = 0.
If a is a root of multiplicity 1 for a polynomial
equation, then a is called a simple root of the polynomial equation.
If P (
x) = 0 has n roots
counted with multiplicity, then also, we see that its degree must be greater
than or equal to n . In other words, “a polynomial equation of degree n
cannot have more than n roots, even if the roots are counted with
their multiplicities”.
One of the important theorems in the theory of equations is the
fundamental theorem of algebra.
As the proof is beyond the scope of the Course, we state it
without proof.
Theorem 3.1 (The Fundamental Theorem of Algebra)
Every polynomial equation of degree n ≥ 1 has at least one root
in C.
Using this, we can prove that a polynomial equation of degree n
has at least n roots in C when the roots are
counted with their multiplicities. This statement together with our discussion
above says that
a polynomial equation of degree n has exactly n roots in
C when the roots are counted with their multiplicities.
Some authors state this statement as the fundamental theorem of
algebra.
(b) Vieta’s Formula
(i) Vieta’s Formula for Polynomial equation of degree 3
Now we obtain these types of relations to higher degree
polynomials. Let us consider a general cubic equation
ax3 + bx2 + cx + d = 0 .
By the fundamental theorem of algebra, it has three roots. Let α , β , and γ be the roots. Thus we
have
ax3 + bx2 + cx + d = a(x − α )(x − β )(x − γ )
Expanding the right hand side, gives
ax3 − a(α + β + γ )x2 + a(αβ + βγ + γα )x − a(αβγ ) .
Comparing the coefficients of like powers, we obtain
α + β + γ = −b/a , αβ + βγ + γα = c/a and αβγ = −d/a
Since the degree of the polynomial equation is 3, we have a ≠ 0 and hence division by a is meaningful. If a monic cubic
polynomial has roots α , β , and γ , then
coefficient of x2 = −(α + β + γ ) ,
coefficient of x = αβ + βγ + γα , and
constant term = −αβγ .
(ii) Vieta’s Formula for Polynomial equation of degree n > 3
The same is true for higher degree monic polynomial equations as
well. If a monic polynomial equation of degree n has roots α1 ,α2 ,...,αn , then

where Σα1 denotes the sum of all roots, Σα1α2 denotes the sum of
product of all roots taken two at a time, Σα1α2α3 denotes the sum of
product of all roots taken three at a time, and so on. If α , β
,γ , and δ are the roots of a quartic equation, then Σα1 is written as Σα
, Σα1α2 is written as Σαβ and so on. Thus we have,
Σα = α + β + γ + δ
Σαβ = αβ + αγ + αδ + βγ + βδ + γδ
Σαβγ = αβγ + αβδ + αγδ + βγδ
Σαβγδ = αβγδ
When the roots are available in explicit numeric form, then also
we use these convenient notations. We have to be careful when handling roots of
higher multiplicity. For instance, if the roots of a cubic equation are 1, 2,
2, then ∑α = 5 and ∑αβ = (1× 2) + (1× 2) + (2 × 2) = 8 .
From the above discussion, we note that for a monic polynomial
equation, the sum of the roots is the coefficient of xn−1 multiplied by (−1) and the product of
the roots is the constant term multiplied by (−1)n .
Example 3.3
If α , β, and γ are the roots of the
equation x3 + px2 + qx + r = 0 , find the value
of 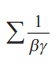 in terms of the coefficients.
in terms of the coefficients.
Solution
Since α , β , and γ are the roots of the
equation x3 + px2 + qx + r = 0 , we have
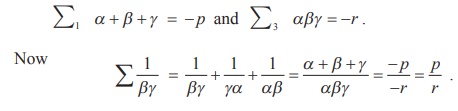
(c) Formation of Polynomial Equations with given Roots
We have constructed quadratic equations when the roots are known.
Now we learn how to form polynomial equations of higher degree when roots are
known. How do we find a polynomial equation of degree n with roots α1 ,α2, …. , αn ? One way of writing a
polynomial equation is multiplication of the factors. That is
( x − α1 )( x − α2 )( x − α3 ) ...( x − αn
) = 0
is a polynomial equation with roots α1 ,α2 ,...,αn. But it is not the
usual way of writing a polynomial equation. We have to write the polynomial
equation in the standard form which involves more computations. But by using
the relations between roots and coefficients, we can write the polynomial
equation directly; moreover, it is possible to write the coefficient of any
particular power of x without finding the entire polynomial equation.
A cubic polynomial equation whose roots are α , β ,
and γ is
x3 − (α + β + γ ) x2 + (αβ + βγ +
γα ) x − αβγ = 0 .
A polynomial equation of degree n with roots α1 ,α2 ,K,αn is given by
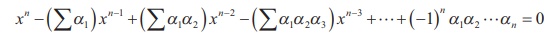
where, ∑α1 , ∑α1α2 , ∑α1α2α3 ,K are as defined
earlier.
For instance, a polynomial equation with roots 1, −2 , and 3 is
given by
x3 − (1− 2 + 3) x2 + (1×(−2) + (−2)× 3 + 3×1) x −1×(−2)×
3 = 0
which, on simplification, becomes x3 − 2x2 − 5x + 6 = 0 .
It is interesting to verify that the expansion of ( x −1)( x +
2)( x − 3) = 0 is x3 − 2x2 − 5x + 6 = 0 .
Example 3.4
Find the sum of the squares of the roots of ax4 + bx3 + cx2 + dx + e = 0 , a ≠ 0
Solution
Let α , β ,γ , and δ be
the roots of ax4 + bx3 + cx2 + dx + e = 0 .
Then, we get

Example 3.5
Find the condition that the roots of cubic equation x3 + ax2 + bx + c=
0 are in the ratio p : q : r .
Solution
Since roots are in the ratio p : q : r , we
can assume the roots as pλ, qλ and rλ,
Then, we get
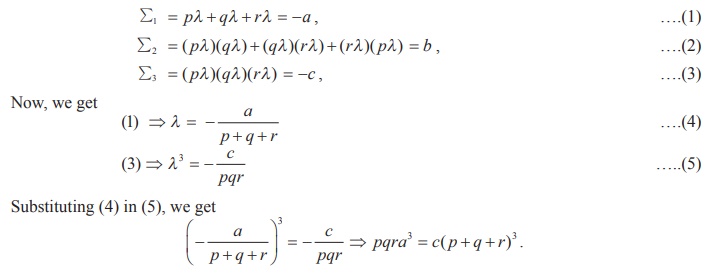
Example 3.6
Form the equation whose roots are the squares of the roots of
the cubic equation
x3 + ax2 + bx + c = 0 .
Solution
Let α , β , and γ be the roots of x3 + ax2 + bx + c = 0 .
Then, we get
Σ1 = α + β + γ = -a , ….(1)
Σ2 = αβ + βγ + γα = b , ….(2)
Σ3 = αβγ = -c . ….(3)
We have to form the equation whose roots are α2 , β2 , and γ2 .
Using (1), (2) and (3), we find the following:
Σ1 = α2 + β2 + γ2 = (α + β + γ )2 - 2(αβ + βγ
+ γα ) = (-a)2 - 2(b) = a2 - 2b ,
Σ2 = α2 β2 + β2γ2 + γ2α2 = (αβ + βγ + γα )2 - 2((αβ )(βγ
) + (βγ )(γα ) + (γα )(αβ ))
= (αβ + βγ + γα )2 - 2αβγ (β +
γ + α ) = (b)2 - 2(-c)(-a) = b2 - 2ca
Σ3 = α2β2γ2 = (αβγ)2 = (-c)2 = c2.
Hence, the required equation is
x3 – (α 2 + β2 + γ2 ) x2 + (α 2 β 2 + β2γ2 + γ2α2 ) x - α2β2γ2 = 0.
That is, x3 - (a2 - 2b) x2 + (b2 - 2ca) x
- c2 = 0.
Example 3.7
If p is real, discuss the nature of the roots of the
equation 4x2 + 4 px + p + 2 = 0 , in terms of p
Solution
The discriminant Δ=(4 p)2 - 4 (4)( p +
2) = 16 ( p2 - p - 2) = 16 ( p +1)( p - 2) . So,
we get
Δ < 0 if -1 < p < 2
Δ = 0 if p = -1 or p = 2
Δ > 0 if -∞ < p < -1 or 2 < p < ∞
Thus the given polynomial has
imaginary roots if -1 < p < 2 ;
equal real roots if p = -1 or p = 2 ;
distinct real roots if -∞ < p < -1 or 2 < p <
∞ .
Related Topics