The Tangent Function and the Inverse Tangent Function

The Tangent Function and the Inverse Tangent Function

We know that the tangent function y = tan x is used to find heights or distances, such as the height of a building, mountain, or flagpole. The domain of y = tan x = sinx/cosx does not include values of x ,  which  make  the  denominator  zero.  So,  the  tangent  function  is  not  defined  at x = …, -3π/2, -π/2, π/2, 3π/2, …. 

Thus, the domain of the tangent function y = tan x is 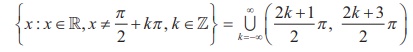 and the range is (−∞, ∞) . The tangent  function y = tan x  has period π.

1. The graph of tangent function

Graph of the tangent function is useful to find the values of the function over the repeated period of intervals. The tangent function is odd and hence the graph of y = tan x is symmetric with respect to the origin.  Since the period of tangent function is π , we need to determine the graph over some interval of length π . Let us consider the interval (-π/2, π/2) and construct the following table to draw the graph of y = tan x, x ∈ (-π/2, π/2).

Now, plot the points and connect them with a smooth curve for a partial graph of  y = tan x , where – π/2  ≤ x ≤ π/2.  If  x  is close to π/2 but remains less than π/2 , the sin x will be close to 1 and cos x will be positive and close to 0. So, as x approaches to π/2 , the ratio sin x/cos x  is positive and large and thus approaching to ∞.

Therefore, the line x = π/2 is a vertical asymptote to the graph. Similarly, if x is approaching to –π/2, the ratio sin x/cos x is negative and large in magnitude and thus, approaching to -∞. So, the line x= - π/2    is also a vertical asymptote to the graph. Hence, we get a branch of the graph of y = tan x for -π/2 < x < -π/2 as shown in the Fig 4.15. The interval (-π/2, π/2) is called the principal domain of y = tan x.

Since the tangent function is defined for all real numbers except at 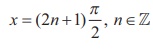, and is increasing , we have vertical asymptotes . 

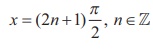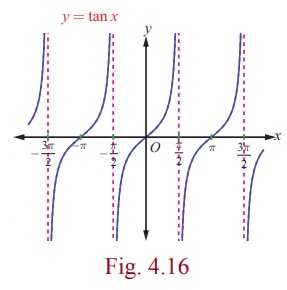
As branches of y = tan x are symmetric with respect to x = nπ , n ∈ Z , the entire graph of y = tan x is shown in  Fig. 4.16.

Note

From the graph, it is seen that y = tan x is positive for 0 < x < π/2 and π < x < 3π/2 ; y = tan x is negative for π/2 < x < π and 3π/2 < x < 2π .

2. Properties of the tangent function

From the graph of y = tan x , we observe the following properties of tangent function.

(i) The graph is not continuous and has discontinuity points at x = (2n +1) π/2 , n ∈ Z 

(ii) The partial graph is symmetric about the origin for – π/2 < x < π/2 .

(iii) It has infinitely many vertical asymptotes x = (2n +1) π/2 , n ∈ Z

(iv) The tangent function has neither maximum nor minimum.

Remark

(i) The graph of y = a tan bx goes through one complete cycle for 

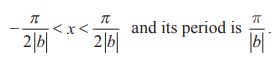
(ii) For y = a tan bx , the asymptotes are the lines 

(iii) Since the tangent function has no maximum and no minimum value, the term amplitude for tan x  cannot be defined.

3. The inverse tangent function and its properties

The tangent function is not one-to-one in the entire domain 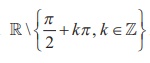 However, tan x : (-π/2, π/2) → R is a bijective function. Now, we define the inverse tangent function with R as its domain and (-π/2, π/2), as its range. 

Definition 4.5

For any real number x, define tan^-1 x as the unique number y in (-π/2, π/2), such that tan y = x.

In other words, the inverse tangent function tan^-1 :  (∞, ∞ )  → (-π/2, π/2), is defined by tan^-1(x) = y if and only if tan y = x and y∈ (-π/2, π/2).

From the definition of y = tan⁻¹ x , we observe the following:

(i) y = tan^-1x if and only if x = tan y for x ∈ R and -π/2 < y < π/2.

(ii) tan (tan^-1 x) = x for any real number  x  and  y = tan^-1 x  is an odd function.

(iii) tan^-1(tan x) = x if and only if – π/2 < x < π/2 . Note that tan^-1(tan π ) = 0 and not π .

Note

(i) Whenever we talk about inverse tangent function, we have,

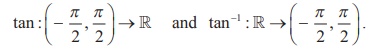
(ii) The restricted domain ( - π/2 , π/2 ) is called the principal domain of tangent function and the values of y = tan^-1 x , x ∈ R , are known as principal values of the function y = tan^-1x .

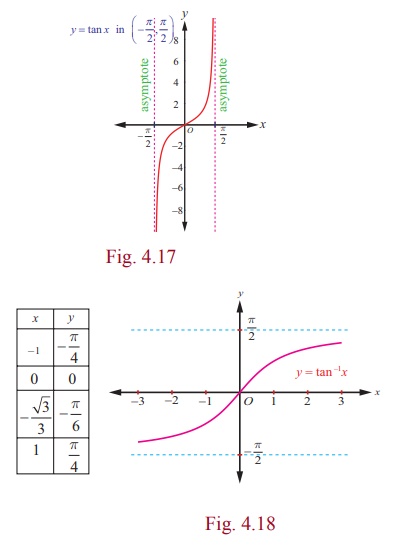
4. Graph of the inverse tangent function

y = tan^-1 x is a function with the entire real line (-∞, ∞) as its domain and whose range is (-π/2, π/2 ) . Note that the tangent function is undefined at – π/2 and at π/2. So, the graph of y = tan^-1x lies strictly between the two lines  y = -π/2 and y = π/2 , and never touches these two lines. In other words, the  two lines  y=-π/2 and y = π/2 are horizontal asymptotes to y = tan^-1x .

Fig. 4.17 and Fig. 4.18 show the graphs of y = tan x in the domain ( - π/2 , π/2 ) and y = tan^-1x in the domain (-∞, ∞) , respectively.

Note

(i) The inverse tangent function is strictly increasing and continuous on the domain (-∞, ∞) .

(ii) The graph of y = tan^-1x  passes through the origin.

(iii) The graph is symmetric with respect to origin and hence, y = tan^-1x is an odd function.

Example 4.8

Find the principal value of tan^-1 (√3)

Solution

Let tan-¹ (√3) = y . 

Then, tan y = √3.

Thus, y = π/3 . Since π/3 ∈ ( - π/2 , π/2 ) .

Thus, the principal value of tan^-1(√3) is π/3.

Example 4.9

Find (i) tan^-1 (-√3 )

(ii) tan^-1 ( tan (3π / 5))

(iii) tan (tan^-1 (2019))

Solution

(iii) Since tan (tan^-1  x) = x, x ∈ R , we have   tan (tan^-1 (2019)) = 2019.

Example 4.10

Find the value of tan^-1 (-1) + cos^-1 ( 1/2 ) + sin^-1 ( - 1/2 ) .

Solution

Let tan^-1 (-1) = y . Then, tan y = -1 = - tan π/4 = tan ( - π/4 ) .

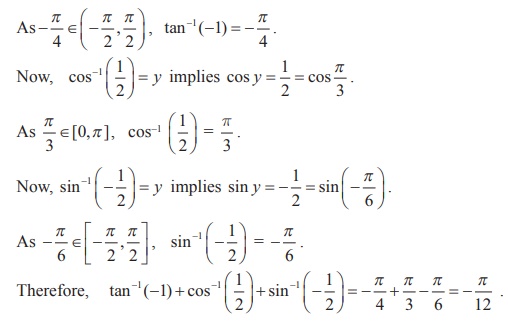
Example 4.11

Prove that   tan (sin^-1 x) = 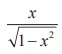, -1 < x < 1

Solution

If x = 0 , then both sides are equal to 0.           ………..(1)

Assume that 0 < x < 1.

Let θ = sin^-1 x . Then  0 < θ < π/2 .  Now, sin θ =  x/1  gives tanθ =  .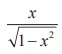

Hence,   tan (sin^-1x) = 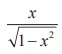           ... (2)

Assume that -1 < x < 0. Then, θ = sin^-1x gives – π/2  < θ < 0. Now, sinθ = x/1 gives tanθ =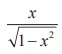 

In this case also,  tan (sin^-1 x) = 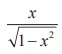       ... (3)

Equations (1), (2) and (3) establish that  tan (sin^-1 x) = 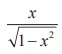 -1 < x < 1.