Chapter: 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Properties of Inverse Trigonometric Functions
Properties of Inverse Trigonometric Functions
In this section, we investigate some properties of inverse
trigonometric functions. The properties to be discussed are valid within the
principal value branches of the corresponding inverse trigonometric functions
and where they are defined.
Property-I

Proof
All the above results follow from the definition of the respective
inverse functions.
For instance, (i) let sinθ = x ; θ ∈ [- π/2 , π/2 ]
Now, sin θ = x gives θ = sin-1 x , by
definition of inverse sine function.
Thus, sin-1 (sinθ ) = θ .
Property-II
(i) sin (sin-1 x) = x , if
x ∈[-1, 1] .
(ii) cos (cos-1 x) = x , if x ∈[-1, 1]
(iii) tan (tan-1 x) = x , if
x ∈ R
(iv) cosec (cosec-1 x) = x , if
x ∈ R \ (-1, 1)
(v) sec(sec-1 x) = x , if x
∈ R \ (-1, 1)
(vi) cot (cot-1 x) = x , if x ∈ R
Proof
(i) For x ∈[-1, 1] , sin-1 x is well
defined.
Let sin-1 x = θ . Then, by definition θ ∈ [- π/2 , π/2 ] and sin θ = x
Thus, sinθ = x implies sin
(sin-1 x) = x
.
Similarly, other results are proved.
Note
For any trigonometric function y = f (x),
we have f ( f -1 (x)) = x for all x in
the range of f . This follows
from the definition
of f -1 (x) .
When we have, f (g-1 (x)),
where g -1 (x) = sin-1 x or cos-1 x, it will
usually be necessary to draw a triangle defined by the inverse trigonometric
function to solve the problem. For instance, to find cot (sin-1 x) , we have
to draw a triangle using sin-1 x. However, we have to be a little
more careful with expression of the
form f -1 ( f (x)).
(ii) Evaluation of f -1[ f (x)] , where f is any
one of the six trigonometric functions.
(a) If x is in the restricted domain (principal domain)
of f , then f -1[ f (x)] = x .
(b) If x is not in the restricted domain of f ,
then find x1 within the restricted domain of f such that f (x)
= f (x1) . Now, f -1[ f (x)] = x1. For
instance,
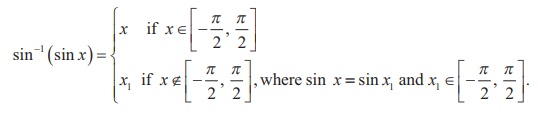
Property-III (Reciprocal inverse identities)
(i) sin-1 ( 1/x ) = cosec x , if x ∈
R \ (-1, 1) .
(ii) cos-1 ( 1/x ). = sec x , if x ∈ R \ (-1, 1) .
(iii) 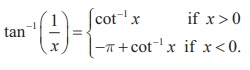
Proof
(i) If x ∈ R \ (-1, 1) ,
then 1/x ∈[-1, 1] and x ≠ 0 .
Thus, sin-1 ( 1/x ) is well
defined.
Let sin-1 ( 1/x ) = θ . Then, by definition θ ∈
[- π/2 , π/2 ] \ {0} and sinθ = 1/x .
Thus, cosecθ = x , which in turn gives θ = cosec-1 x .
Now, sin-1 ( 1/x ) = θ = cosec-1 x . Thus, sin-1 ( 1/x ) = cosec-1 x , x ∈
R \ (-1, 1).
Similarly, other results are proved.
Property-IV (Reflection identities)
(i) sin-1 (-x) = - sin-1x , if x ∈ [-1, 1] .
(ii) tan-1 (-x) = - tan-1 x , if x ∈ R .
(iii) cosec-1 (-x) = - cosec-1 x , if |x| ≥ 1 or x ∈
R \ (-1, 1).
(iv) cos-1 (-x) = π - cos-1 x , if x ∈[-1, 1] .
(v) sec-1 (-x) = π - sec-1 x , if |x| ≥ 1 or x ∈
R \ (-1, 1) .
(vi) cot-1 (-x) = π - cot-1 x , if x ∈ R .
Proof
(i) If x ∈[-1, 1] , then -x ∈[-1,
1] . Thus, sin-1 (-x) is well defined
Let sin-1 (-x) = θ . Then θ ∈ [- π/2 , π/2 ] and sinθ
= -x .
Now, sinθ = -x gives x = -sinθ = sin(-θ )
From x = sin(-θ ) , we must have sin-1 x = -θ , which in turn
gives θ = -sin-1 x .
Hence, sin-1 (-x) = -sin-1 x .
(iv) If x ∈[-1, 1] , then -x ∈[-1,
1] . Thus, cos-1 (-x) is well defined
Let cos-1 (-x) = θ . Then θ ∈[0, π ] and cos θ = -x .
Now, cosθ = -x implies x = -cosθ = cos (π -θ ) .
Thus, π -θ = cos-1 x, which gives θ = π - cos-1 x .
Hence, cos-1 (-x) = π - cos-1 x .
Similarly, other results are proved.
Note
(i) The inverse function of an one-to-one and odd function is also
an odd function. For instance, y = sin-1 x is an odd function, since sine
function is both one-to-one and odd in the restricted domain [- π/2 , π/2 ] .
(ii) Is the inverse function of an even function also even? It
turns out that the question does not make sense, because an even function
cannot be one-to-one if it is defined anywhere other than 0. Observe that cos-1 x and sec-1 x are not even
functions.
Property-V ( Cofunction inverse identities )
(i) sin-1 x + cos-1 x = π/2 , x ∈[-1, 1].
(ii) tan-1 x + cot-1 x = π/2 , x ∈ R.
(iii) cosec-1 x + sec-1 x = π/2, x ∈ R \ (-1, 1) or
|x| ≥ 1.
Proof
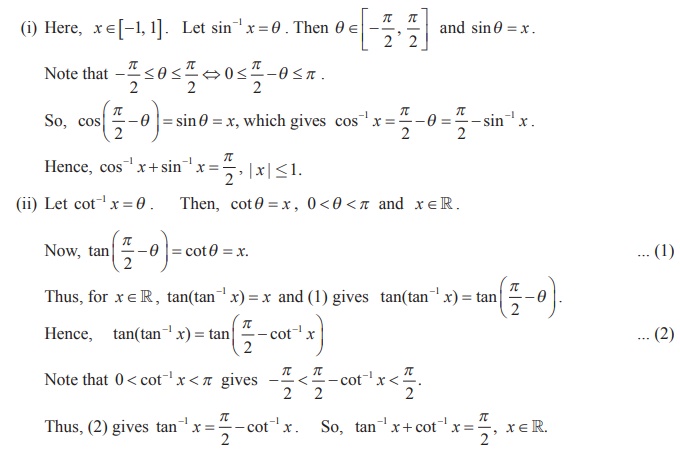
Similarly, (iii) can be proved.
Property-VI
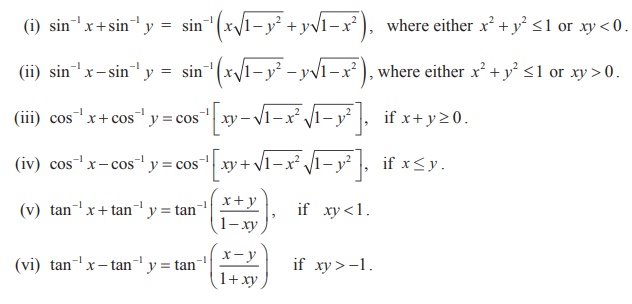
Proof
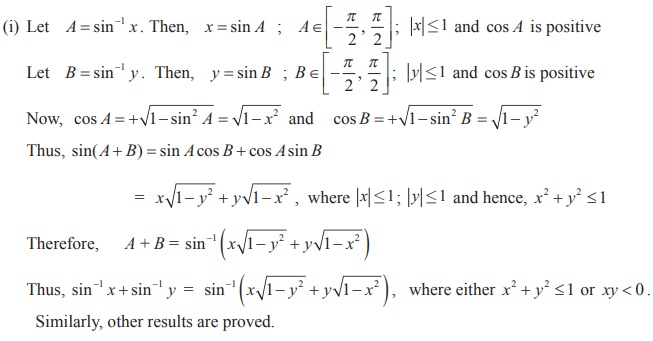
Property-VII

Proof
(i) By taking y x = in Property-VI (v) , we get the desired result
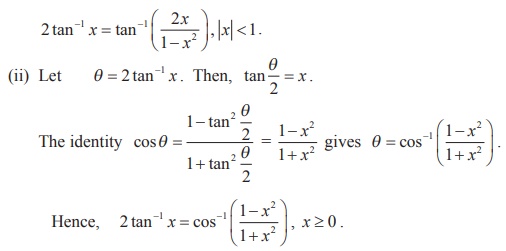
Similarly, other results are proved.
Property-VIII

Proof
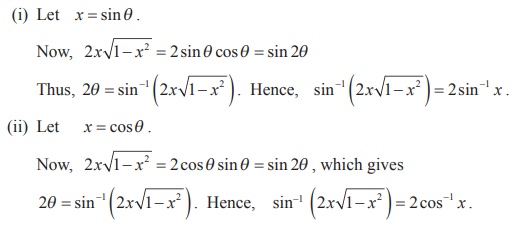
Property-IX
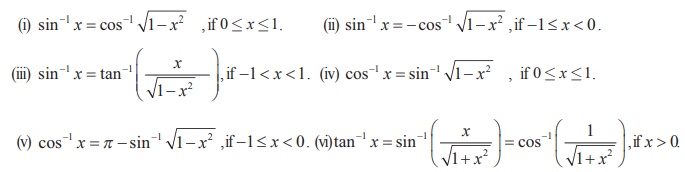
Proof
(i) Let sin-1 x = θ . Then, sin
θ = x . Since 0 ≤ x
≤1 , we get 0 ≤ θ ≤ π/2 .
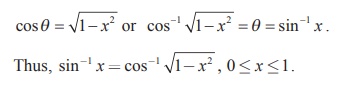
(ii) Suppose that -1 ≤ x ≤ 0 and sin-1 x = θ .
Then - π /2 ≤ θ < 0
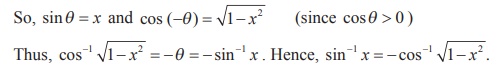
Similarly, other results are proved.
Property-X
(i) 3sin-1 x = sin-1 (3x - 4x3 ) , x ∈ [- 1/2 , 1/2 ] .
(ii) 3cos-1 x = cos-1 (4x3 - 3x) , x ∈ [ 1/2 , 1]
Proof
(i) Let x = sin θ . Thus, θ = sin-1x .
Now, 3x - 4x3 = 3sinθ - 4 sin3 θ = sin 3θ .
Thus, sin-1 (3x - 4x3 ) = 3θ = 3sin-1x .
The other result is proved in a similar way.
Remark
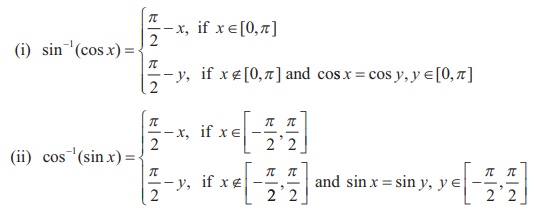
Related Topics