with Answers, Solution - Solved Example Problems on Inverse Trigonometric Functions | 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Chapter: 12th Mathematics : UNIT 4 : Inverse Trigonometric Functions
Solved Example Problems on Inverse Trigonometric Functions
Sine Function and Inverse Sine Function
Example 4.1
Find the principal value of sin-1 ( - 1/2 ) (in radians and degrees).
Solution
Let sin-1 ( - 1/2 ) = y . Then sin y = - 1/2 .
The range of the principal value of sin-1 x is [- π/2 , π/2 ] and hence, let us find y ∈ [- π/2 , π/2 ] such that sin y = - 1/2 . Clearly, y = - π /6.
Thus, the principal value of sin-1 ( - 1/2 ) is – π/6 . This corresponds to − 30°.
Example 4.2
Find the principal value of sin-1 (2) , if it exists.
Solution
Since the domain of y = sin-1 x is [-1, 1] and 2 ∈ [-1, 1] , sin-1 (2) does not exist.
Example 4.3
Find the principal value of
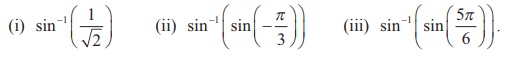
Solution
We know that sin-1 : [-1, 1] → [- π/2 , π/2] is given by
sin-1 x = y if and only if x = sin y for -1 ≤ x ≤ 1 and π/2 ≤ y ≤ π/2 . Thus,
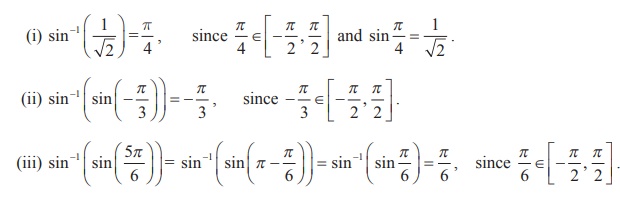
Example 4.4
Find the domain of sin-1 (2 - 3x2)
Solution
We know that the domain of sin-1 ( x) is [-1, 1].
This leads to -1 ≤ 2 - 3x2 ≤ 1, which implies - 3 ≤ -3x2 ≤ -1.
Now, - 3 ≤ -3x2 , gives x2 ≤ 1 and ... (1)
-3x2 ≤ -1 , gives x2 ≥ 1/3 ... (2)
Combining the equations (1) and (2), we get 1/3 ≤ x2 ≤ 1 . That is, 1/√3 ≤ |x| ≤ 1, which gives
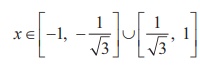 , since a ≤ |x| ≤ b implies x ∈ [-b, - a]U[a, b].
, since a ≤ |x| ≤ b implies x ∈ [-b, - a]U[a, b].
The Cosine Function and Inverse Cosine Function
Example 4.5
Find the principal value of cos-1 ( √3 / 2 ) .
Solution
Let cos-1 (√3 / 2 ) = y . Then, cos y = √3 / 2.
The range of the principal values of y = cos-1 x is [0, π ].
So, let us find y in [0, π ] such that cos y = √3 / 2
But, cos π/6 = √3/2 and π/6 ∈ [0,π ]. Therefore, y = π /6
Thus, the principal value of cos-1 (√3/2 ) is π/6 .
Example 4.6
Find

Solution
It is known that cos-1 x : [-1, 1] → [0, π ] is given by
cos-1 x = y if and only if x = cos y for -1 ≤ x ≤ 1 and 0 ≤ y ≤ π .
Thus, we have
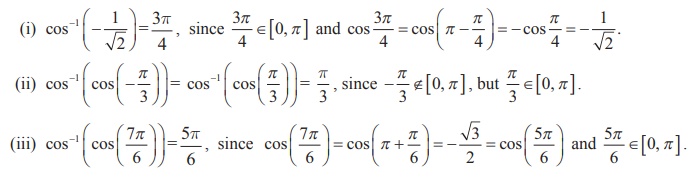
Example 4.7
Find the domain of cos-1 ( [2 + sin x] /3 ) .
Solution
By definition, the domain of y = cos-1 x is -1 ≤ x ≤ 1 or |x| ≤1 . This leads to
-1 ≤ [2 + sin x]/3 ≤ 1 which is same as - 3 ≤ 2 + sin x ≤ 3 .
So, - 5 ≤ sin x ≤ 1 reduces to -1 ≤ sin x ≤ 1, which gives
- sin-1 (1) ≤ x ≤ sin-1 (1) or π/2 ≤ x ≤ π/2 .
Thus, the domain of cos-1 ( [2 + sin x] /3 ) is [- π/2 , π/2 ] .
The Tangent Function and the Inverse Tangent Function
Example 4.8
Find the principal value of tan-1 (√3)
Solution
Let tan-1 (√3) = y .
Then, tan y = √3.
Thus, y = π/3 . Since π/3 ∈ ( - π/2 , π/2 ) .
Thus, the principal value of tan-1(√3) is π/3.
Example 4.9
Find (i) tan-1 (-√3 )
(ii) tan-1 ( tan (3π / 5))
(iii) tan (tan-1 (2019))
Solution
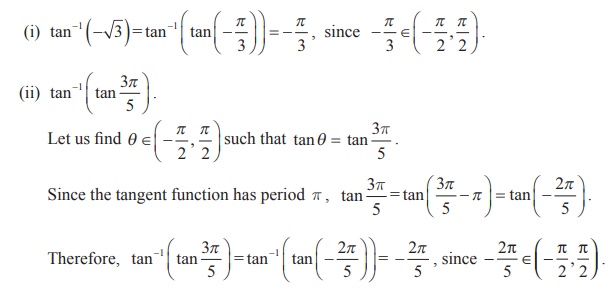
(iii) Since tan (tan-1 x) = x, x ∈ R , we have tan (tan-1 (2019)) = 2019.
Example 4.10
Find the value of tan-1 (-1) + cos-1 ( 1/2 ) + sin-1 ( - 1/2 ) .
Solution
Let tan-1 (-1) = y . Then, tan y = -1 = - tan π/4 = tan ( - π/4 ) .
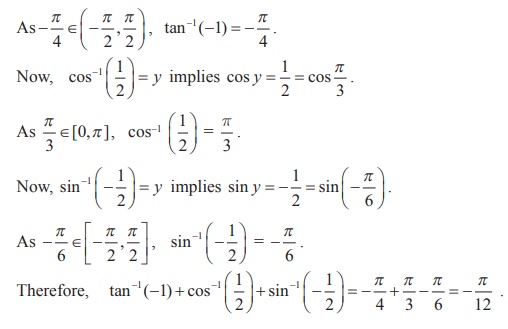
Example 4.11
Prove that tan (sin-1 x) = 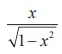 , -1 < x < 1
, -1 < x < 1
Solution
If x = 0 , then both sides are equal to 0. ………..(1)
Assume that 0 < x < 1.
Let θ = sin-1 x . Then 0 < θ < π/2 . Now, sin θ = x/1 gives tanθ = 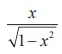 .
.
Hence, tan (sin-1x) = 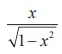 ... (2)
... (2)
Assume that -1 < x < 0. Then, θ = sin-1x gives – π/2 < θ < 0. Now, sinθ = x/1 gives tanθ = 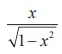
In this case also, tan (sin-1 x) = 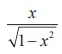 ... (3)
... (3)
Equations (1), (2) and (3) establish that tan (sin-1 x) = 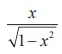 -1 < x < 1.
-1 < x < 1.
Principal Value of Inverse Trigonometric Functions
Example 4.12
Find the principal value of
(i) cosec-1 (-1) (ii) sec-1 (-2) .
Solution
(i) Let cosec-1 (-1) = y . Then, cosec y = -1
Since the range of principal value branch of y= cosec-1 x is [- π/2 , π/2] \ {0} and
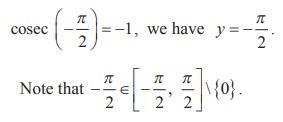
Thus, the principal value of cosec-1 (-1) is – π/2 .
(ii) Let y = sec-1 (-2) . Then, sec y = -2 .
By definition, the range of the principal value branch of y = sec-1 x is [0,π ]\ {π /2} .
Let us find y in [0,π ] – {π/2} such that sec y = -2 .
But, sec y = −2 ⇒ cos y = − 1/2 .
Now, cos y =- 1/2 = -cos π/3 = cos (π – π/3 ) = cos 2π/3 . Therefore, y = 2π/3 .
Since 2π/3 ∈ [0, π ] \ {π/2 } , the principal value of sec-1 (-2) is 2π/3 .
Example 4.13
Find the value of sec-1(- 2√3 / 2)
Solution
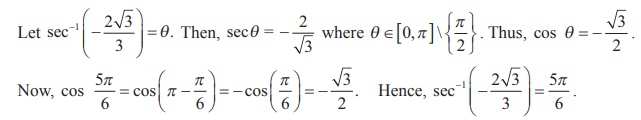
Example 4.14
If cot-1 ( 1/7 ) = θ , find the value of cos θ .
Solution
By definition, cot−1 x ∈ (0, π) .
Therefore, cot-1 (1/7) = θ implies cot θ ∈ (0,π ) .
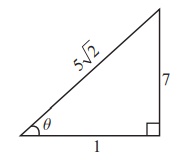
But cot-1 ( 1/7 ) = θ implies cot θ = 1/7 and hence tan θ = 7 and θ is acute.
Using tan θ = 7/1 , we construct a right triangle as shown . Then, we have, cosθ = 1/ 5√2 .
Example 4.15
Show that 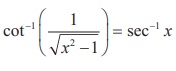 , x > 1 .
, x > 1 .
Solution
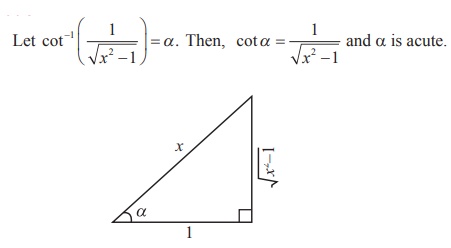
We construct a right triangle with the given data.
From the triangle, secα = x/1 = x . Thus, α = sec-1 x .
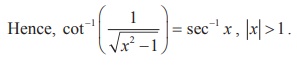
Example 4.16
Prove that 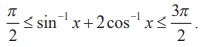
Solution
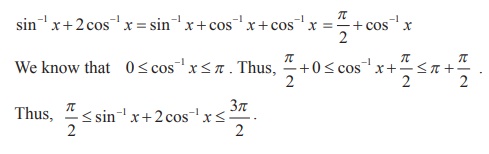
Example 4.17
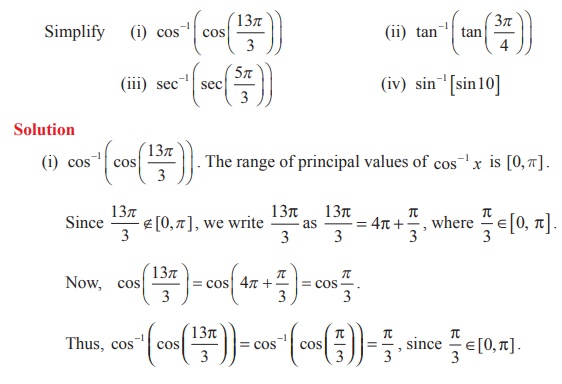

Example 4.18
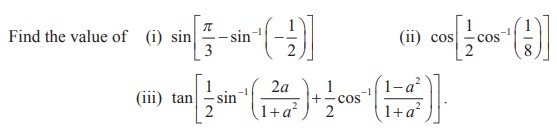
Solution
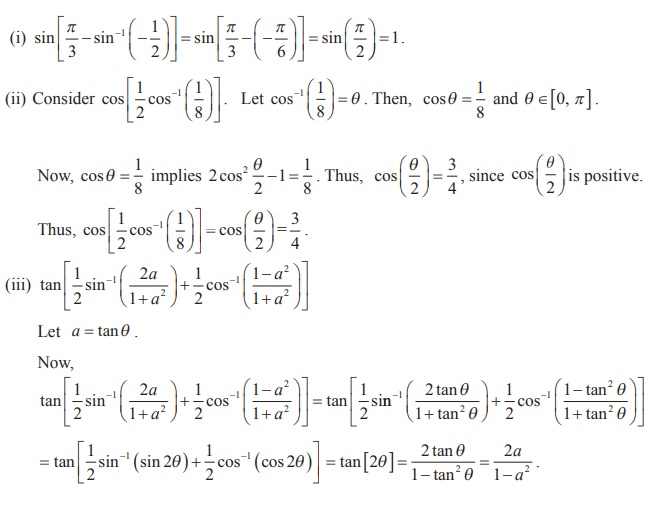
Example 4.19
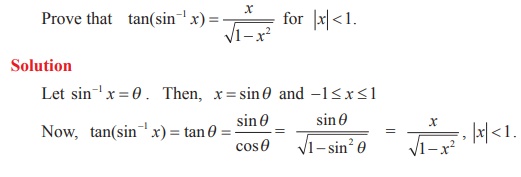
Example 4.20
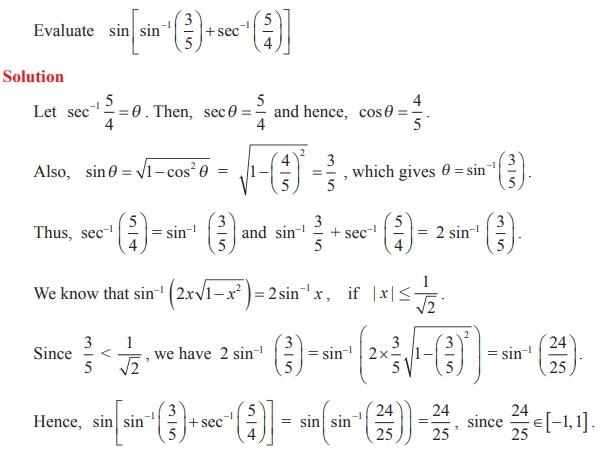
Example 4.21
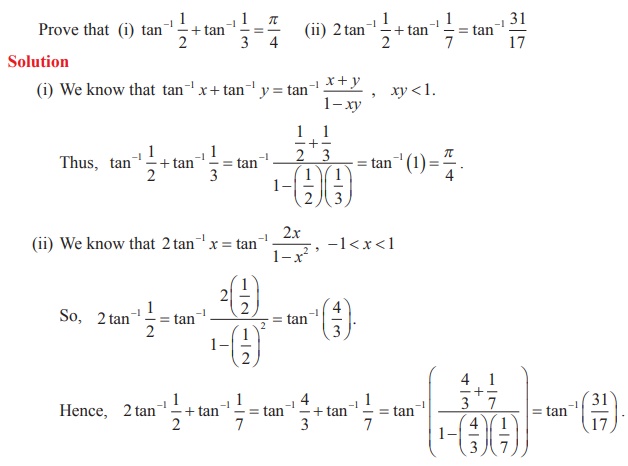
Example 4.22
If cos-1 x + cos-1 y + cos-1 z = π and
0 < x, y, z < 1, show that
x2 + y2 + z2 + 2xyz = 1
Solution
Let cos-1 x = α and cos-1 y = β . Then, x = cosα and y = cos β .
cos-1 x + cos-1 y + cos-1 z = π gives
α + β = π -
cos-1 z.
... (1)
Now, cos (α + β ) = cosα cos β - sin
α sin β = xy – √[1-x2] √[1-y2]
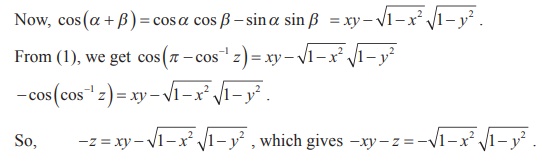
Squaring on both sides and simplifying, we get x2 + y2 + z2 + 2xyz = 1.
Example 4.23
If a1, a2, a3, ... an is an arithmetic progression with common difference d, prove that
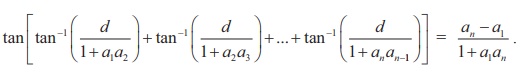
Solution
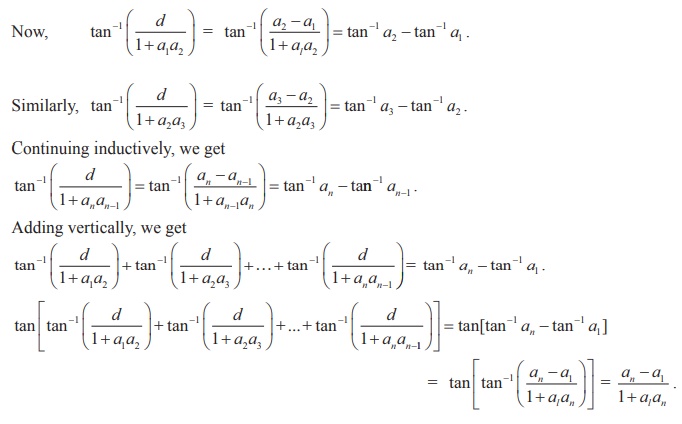
Example 4.24
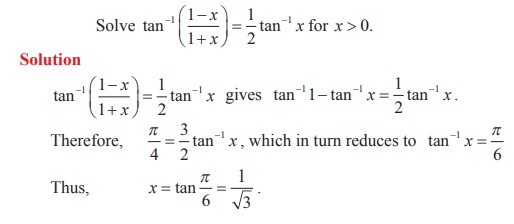
Example 4.25
Solve sin-1 x > cos-1 x
Solution
Given that sin-1 x > cos-1 x . Note that
-1 ≤ x ≤ 1.
Adding both sides by sin-1 x, we get
sin-1 x + sin-1 x > cos-1 x + sin-1 x , which
reduces to 2 sin-1 x > π/2 .
As sine function increases in the interval [- π/2 , π/2
] , we have x > sin π/4 or x > 1/√2.
Thus, the solution set is the interval ( 1/√2, 1 ].
Example 4.26
Show that cot(sin-1 x) = 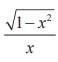 , -1 ≤ x ≤ 1 and x ≠
0
, -1 ≤ x ≤ 1 and x ≠
0
Solution
Let sin-1 x = θ .
Then, x = sin θ and x ± 0, we get θ ∈ [ -π/2, 0) U ( 0, π/2].
Hence, cos θ ≥ 0 and
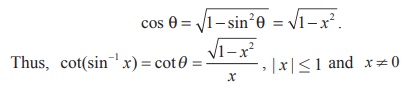
Example 4.27
Solve tan-1 2x + tan-1 3x = π/4 , if 6x2 < 1.
Solution
Now, tan-1 2x + tan-13x = tan-1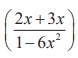 , since 6x2 < 1 .
, since 6x2 < 1 .
So, tan-1 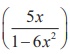 = π/4
, which implies 5x/ [1- 6x2] = tan π /4 = 1
= π/4
, which implies 5x/ [1- 6x2] = tan π /4 = 1
Thus, 1- 6x2 = 5x , which
gives 6x2 + 5x -1 = 0
Hence, x =
1/6 , -1 . But x = -1 does not satisfy 6x2 < 1 .
Observe that x =
-1 makes the left side of the equation negative whereas the right side is a positive number. Thus,
x = -1 is not a solution.
Hence, x = 1/6 is the only solution of the equation.
Example 4.28
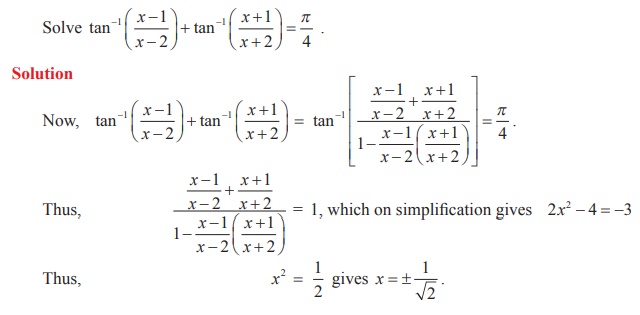
Example 4.29
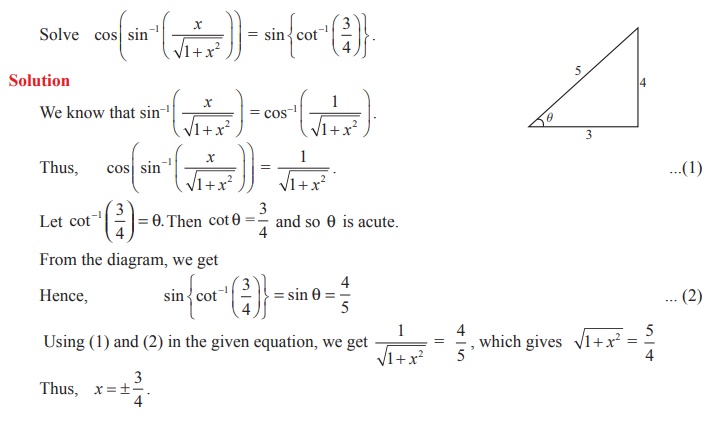
Related Topics