Some Fundamental Concepts of Inverse Trigonometric Functions

Some Fundamental Concepts

Definition 4.1 (Periodicity)

A real valued function f is periodic if there exists a number p > 0 such that for all x in the domain of f , x + p is in the domain of f and f (x + p) = f (x) .

The smallest of all such numbers, is called the period of the function f .

For instance, sin x, cos x, cosecx , sec x and e^ix are periodic functions with period 2π radians, whereas tan x and cot x are periodic functions with period π radians.

Definition 4.2 (Odd and Even functions)

A real valued function f is an even function if for all x in the domain of f , −x is also in the domain of f and f (−x) = f (x) .

A real valued function f is an odd function if for all x in the domain of f , −x is also in  the domain of f and f (−x) = − f (x) .

For instance, x³ , sin x, cosec x, tan x and cot x are all odd functions, whereas x², cos x and sec x are even functions.

Remark

The period of f = g ± h is lcm{period of g, period of h } , whenever they exist.

For instance, the period of y = cos 6x + sin 4x is π and that of y = cos x - sin x is 2 π

1. Domain and Range of trigonometric functions

The domain and range of trigonometric functions are given in the following table.

2. Graphs of functions

Let f : R → R be a real valued function and f (x) be the value of the function f at a point x in the domain. Then, the set of all points ( x, f (x)), x ∈ R determines the graph of the function f . In general, a graph in xy -plane need not represent a function. However, if the graph passes the vertical line test (any vertical line intersects the graph, if it does, atmost at one point), then the graph represents a function. A best way to study a function is to draw its graph and analyse its properties through the graph.

Every day, we come across many phenomena like tides, day or night cycle, which involve periodicity over time. Since trigonometric functions are periodic, such phenomena can be studied through trigonometric functions. Making a visual representation of a trigonometric function, in the form of a graph, can help us to analyse the properties of phenomena involving periodicities.

To graph the trigonometric functions in the xy -plane, we use the symbol x for the independent variable representing an angle measure in radians, and y for the dependent variable. We write y =  sin x to represent the sine function, and in a similar way for other trigonometric functions. In the following sections, we discuss how to draw the graphs of trigonometric functions and inverse trigonometric functions and study their properties.

3. Amplitude and Period of a graph

The amplitude is the maximum distance of the graph from the x -axis. Thus, the amplitude of a function is the height from the x -axis to its maximum or minimum. The period is the distance required for the function to complete one full cycle.

Remark

(i) The graph of a periodic function consists of repetitions of the portion of the graph on an interval of length of its period.

(ii) The graph of an odd function is symmetric with respect to the origin and the graph of an even function is symmetric about the y -axis.

4. Inverse functions

Remember that a function is a rule that, given one value, always gives back a unique value as its answer. For existence, the inverse of a function has to satisfy the above functional requirement. Let us explain this with the help of an example.

Let us consider a set of all human beings not containing identical twins. Every human being from our set, has a blood type and a DNA sequence. These are functions, where a person is the input and the output is blood type or DNA sequence. We know that many people have the same blood type but DNA sequence is unique to each individual. Can we map backwards? For instance, if you know the blood type, do you know specifically which person it came from? The answer is NO. On the other hand, if you know a DNA sequence, a unique individual from our set corresponds to the known DNA sequence. When a function is one-to-one, like the DNA example, then mapping backward is possible. The reverse mapping is called the inverse function. Roughly speaking, the inverse function undoes what the function does.

For any right triangle, given one acute angle and the length of one side, we figure out what the other angles and sides are. But, if we are given only two sides of a right triangle, we need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric

function comes into play.

We know that none of the trigonometric functions is one-to-one over its entire domain. For instance , given sinθ = 0.5 , we have infinitely many θ = 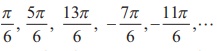  satisfying the equation. Thus, given sinθ , it is not possible to recover θ uniquely. To overcome the problem of having multiple angles mapping to the same value, we will restrict our domain suitably before defining the inverse trigonometric function.

To construct the inverse of a trigonometric function, we take an interval small enough such that the function is one-to-one in the restricted interval, but the range of the function restricted to that interval is the whole range. In this chapter, we define the inverses of trigonometric functions with their restricted domains.

5. Graphs of inverse functions

Assume that f is a bijective function and  f ⁻¹ is the inverse of  f . Then,  y = f (x) if and only if x = f ⁻¹ ( y) . Therefore, (a, b) is a point on the graph of f if and only if (b, a) is the corresponding point on the graph of f⁻¹ . This suggests that graph of the inverse function f ⁻¹ is obtained from the graph of f  by interchanging x and y axes. In other words, the graph of f ⁻¹ is the mirror image of the graph of f in the line y = x or equivalently, the graph of f ⁻¹ is the reflection of the graph of f in the line y = x.