Sine Function and Inverse Sine Function

Sine Function and Inverse Sine Function

Let us recall that sine function is a function with R as its domain and [−1, 1] as its range. We write y = sin x and y = sin⁻¹x or y = arcsin(x) to represent the sine function and the inverse sine function, respectively. Here, the symbol −1 is not an exponent. It denotes the inverse and does not mean the reciprocal.

We know that sin ( x + 2π ) = sin x is true for all real numbers x . Also, sin ( x + p) need not be equal to sin x for 0 < p < 2π and for all x . Hence, the period of the sine function is 2 π

1. The graph of sine function

The graph of the sine function is the graph of y = sin x , where x is a real number. Since sine function is periodic with period 2π , the graph of the sine function is repeating the same pattern in each of the intervals …, [-2π,0], [0,2π], [2π,4π], [4π,6π], …. Therefore, it suffices to determine the portion of the graph for x ∈ [0, 2π ]. Let us construct the following table to identify some known coordinate pairs for the points (x, y) on the graph of y = sin x , x ∈[0, 2π ].

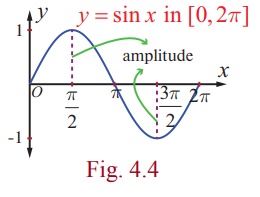
It is clear that the graph of y = sin x , 0 ≤ x ≤ 2π , begins at the origin. As x increases from 0 to π/2 , the value of y = sin x increases from 0 to 1. As x increases from π/2 to π and then to 3 π/2 , the value of  y  decreases from 1 to 0 and then to -1. As  x increases from 3 π/2  to 2 π, the value of y increases from -1 to 0. Plot the points listed in the table and connect them with a smooth curve. The portion of the graph is shown in Fig. 4.4.

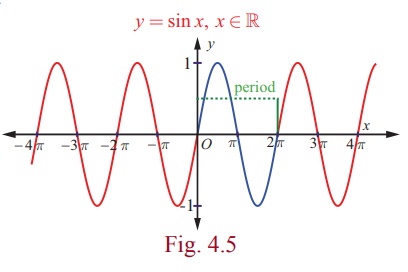
The  entire graph of y = sin x , x ∈ R consists of repetitions of the above portion on either side of the interval [0, 2π ] as y = sin x is periodic with period 2 π. The graph of sine function is shown in Fig. 4.5. The portion of the curve corresponding to 0 to 2π is called a cycle. Its amplitude is 1.

Note

Observe that sin x ≥ 0 for 0 ≤ x ≤ π , which corresponds to the values of the sine function in quadrants I and II and sin x < 0 for π < x < 2π , which corresponds to the values of the sine function in quadrants III and IV.

2. Properties of the sine function

From the graph of y = sin x , we observe the following properties of sine function:

·            There is no break or discontinuities in the curve. The sine function is continuous.

·            The sine function is odd, since the graph is symmetric with respect to the origin.

·            The maximum value of sine function is 1 and occurs at x = …3π / 2, π / 2, 5π / 2, , ….  and the minimum value is −1 and occurs at x = … , - π / 2, 3π / 2,, 7π / 2,… In otherwords, −1 ≤ sin x ≤ 1 for all x ∈  R.

3. The inverse sine function and its properties

The sine function is not one-to-one in the entire domain R . This is visualized from the fact that every horizontal line y = b, -1 < b < 1, intersects the graph of y = sin x infinitely many times. In other words , the sine function does not pass the horizontal line test, which is a tool to decide the one-to-one status of a function. If the domain is restricted to [ -π/2, π/2 ] then the sine function becomes one to one and onto (bijection) with the range [−1, 1]. Now, let us define the inverse sine function with [−1, 1] as its domain and with [ -π/2, π/2 ] , as its range.

Definition 4.3

For  -1 ≤  x ≤ 1,  define sin^-1x as the unique number  y  in [ -π/2, π/2 ]  such that sin y = x . In other words, the inverse sine function  sin^-1  : [-1, 1]  → [ -π/2, π/2 ]    is defined by  sin^-1 (x) = y if and only if sin y = x  and  y ∈ [ -π/2, π/2 ] 

Note

(i) The sine function is one-to-one on the restricted domain [ -π/2, π/2 ] , but not on any larger

interval containing the origin.

(ii) The cosine function is non-negative on the interval [ -π/2, π/2 ] , the range of sin^-1x . This observation is very important for some of the trigonometric substitutions in Integral Calculus.

(iii) Whenever we talk about the inverse sine function, we have,

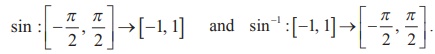
(iv) We can also restrict the domain of the sine function to any one of the intervals,

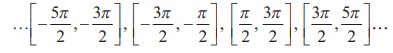 where it is one-to-one and its range is [-1,1] .

(vi) The restricted domain [ -π/2, π/2 ] is called the principal domain of sine function and the values

of y = sin^-1 x , -1 ≤ x ≤ 1, are known as principal values of the function y = sin^-1x .

From the definition of y = sin^-1x , we observe the following:

(i) y = sin^-1x if and only if x = sin y for -1 ≤ x ≤ 1 and -π/2 ≤ y ≤ π/2.

(ii)  sin (sin^-1 x) = x  if |x| ≤ 1 and has no sense if |x| > 1 .

(iii) sin^-1 (sin x) = x if  - π/2  ≤ x ≤  π/2. Note that  sin^-1 (sin 2 π) = 0 ≠ 2 π .

(iv) sin^-1 (sin x) = π – x if π /2 ≤ x ≤  3π/2. Note that - ≤ π - x ≤ π/2.

(v) y = sin^-1 x is an odd function.

Remark

Let us distinguish between the equations sin x = 1/2 and x = sin^-1 (1/2). To solve the equation sin x = 1/2, one has to find all values of x in the interval (-∞, ∞) such that sin x = 1/2 . However, to find x in x = sin^-1 ( 1/2 ) , one has to find the unique value x in the interval [- π/2 , π/2 ] such that sin x = 1/2.

4. Graph of the inverse sine function

The inverse sine function, sin−1 : [−1, 1] → [-π/2 , π/2],  receives a real number x in the interval [−1, 1] as input and gives a real number y in the interval  [-π/2 , π/2] as output. As usual, let us find some points (x, y) using the equation y = sin⁻¹ x and plot them in the xy -plane. Observe that the value of y increases from - π/2 to π/2 as x increases from −1 to 1. By connecting these points by a smooth curve, we get the graph of y = sin⁻¹ x as shown in Fig. 4.6.

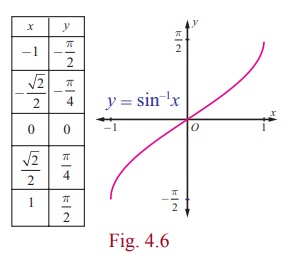
Note

The graph of y = sin⁻¹ x

(i) is also obtained by reflecting the portion of the entire graph of y = sin x in the interval [- π/2 , π/2 ] about the line y = x or by interchanging x and y axes from the graph of y = sin x .

(ii) passes through the origin.

(iii) is symmetric with respect to the origin and hence, y = sin^-1 x is an odd function.

We  depict the graphs of both   y =  sin x, - π/2 ≤ x ≤ π/2 and y = sin^-1 x, -1 ≤ x ≤ 1 together for a better understanding.

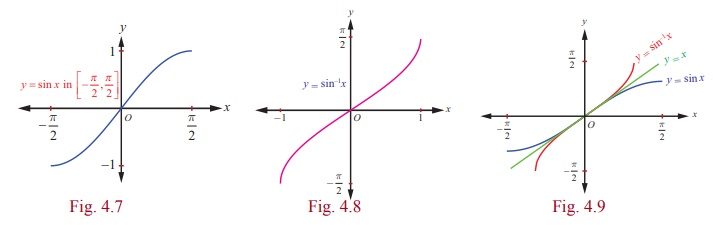
Fig. 4.9 illustrates that the graph of y = sin^-1 x is the mirror image of the graph of y = sin x, - π/2 ≤ x ≤ π/2, in the line y = x and also shows that the sine function and the inverse sine function are symmetric with respect to the origin.

Example 4.1

Find the principal value of sin^-1 ( - 1/2 ) (in radians and degrees).

Solution

Let sin^-1 ( - 1/2 ) = y . Then sin y = - 1/2 .

The range of the principal value of sin^-1 x is [- π/2 , π/2 ] and hence, let us find y ∈ [- π/2 , π/2 ] such that sin y = - 1/2 . Clearly, y = - π /6.

Thus, the principal value of sin^-1 ( - 1/2 ) is – π/6 . This corresponds to − 30°.

Example 4.2

Find the principal value of sin^-1 (2) , if it exists.

Solution

Since the domain of y = sin^-1 x is [-1, 1] and 2 ∈  [-1, 1] , sin^-1 (2) does not exist.

Example 4.3

Find the principal value of 

Solution

We know that sin^-1 : [-1, 1] → [- π/2 , π/2] is given by

sin^-1 x = y if and only if x = sin y for -1 ≤ x ≤ 1 and  π/2 ≤ y ≤ π/2 . Thus,

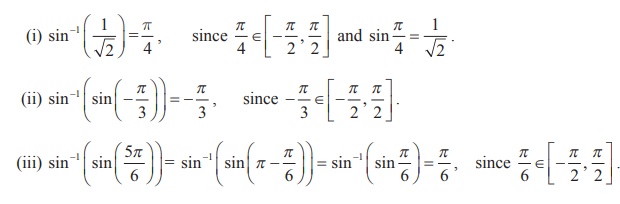
Example 4.4

Find the domain of sin^-1 (2 - 3x²)

Solution

We know that the domain of sin^-1 ( x) is [-1, 1].

This leads to -1 ≤ 2 - 3x² ≤ 1, which implies - 3 ≤ -3x² ≤ -1.

Now, - 3 ≤ -3x² ,  gives x² ≤ 1 and ... (1)

-3x²  ≤ -1 ,  gives x²  ≥ 1/3 ... (2)

Combining the equations (1) and (2), we get 1/3  ≤ x² ≤ 1 . That is, 1/√3  ≤ |x| ≤ 1, which gives

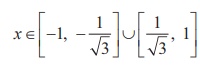, since a ≤  |x| ≤ b implies x ∈ [-b, - a]U[a, b].